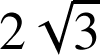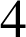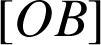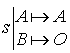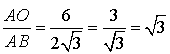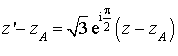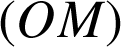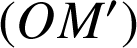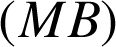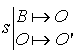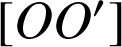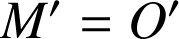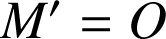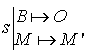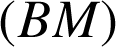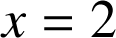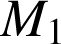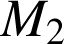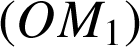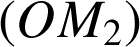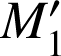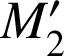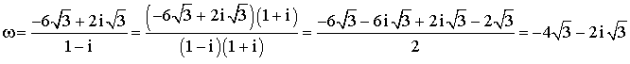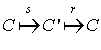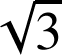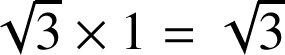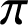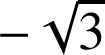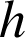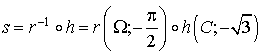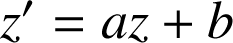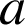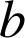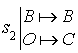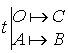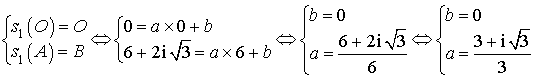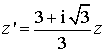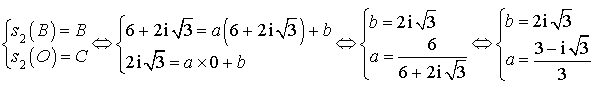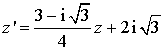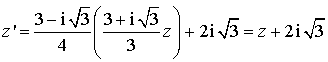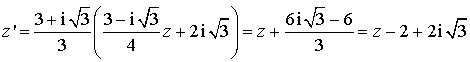Introduction
Prérequis : Cours de spécialité mathématiques sur les similitudes directes.
Durée : 90 minutes
Niveau : facile
Énoncé de l'exercice
Le plan est rapporté au repère orthonormé direct ![]() .
.
Soit
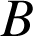 le point de coordonnées
le point de coordonnées ![]() . Les points
. Les points
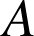 et
et
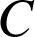 sont les projetés orthogonaux respectifs de
sont les projetés orthogonaux respectifs de
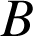 sur les axes
sur les axes ![]() et
et ![]() . Soit
. Soit ![]() le cercle de diamètre
le cercle de diamètre ![]() et
et
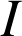 son centre.
son centre.
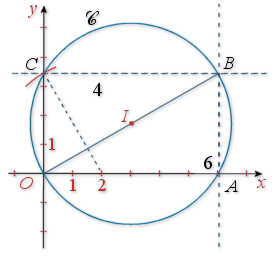
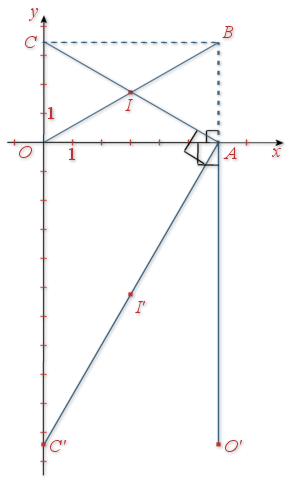
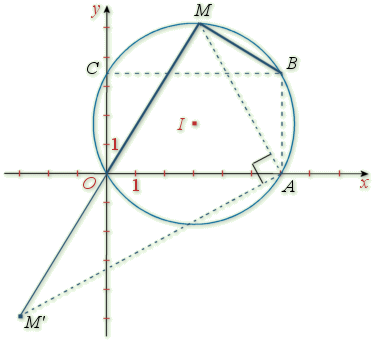
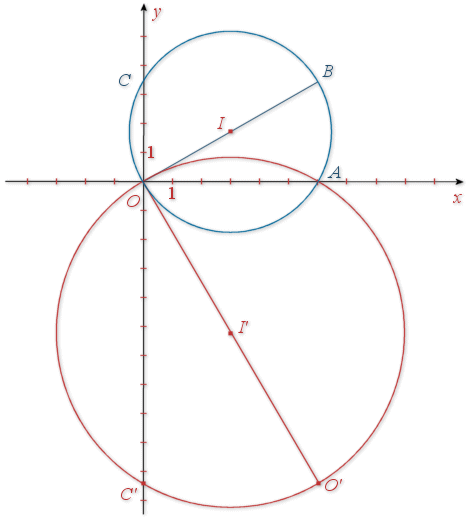
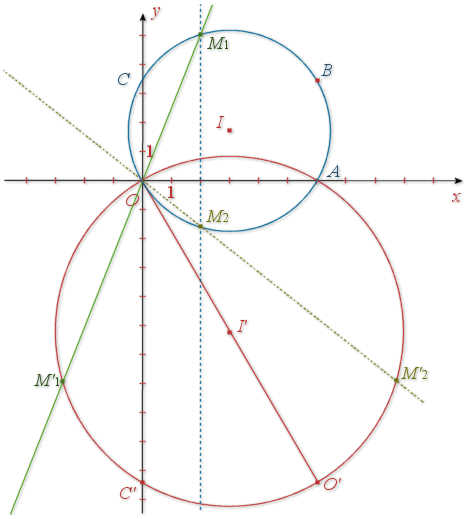
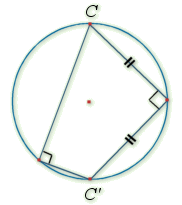
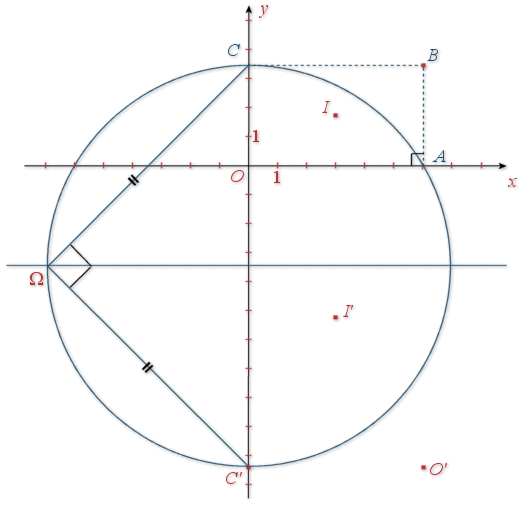
1) Faire une figure à compléter au fur et à mesure des questions en prenant 1 cm pour unité graphique (on pourra remarquer que ![]() pour construire
pour construire
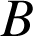 ) et déterminer les affixes des points
) et déterminer les affixes des points
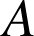 ,
,
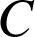 et
et
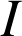 .
.
2) Soit
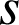 la similitude directe de centre
la similitude directe de centre
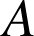 qui transforme
qui transforme
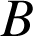 en
en
 .
.
a. Déterminer l'angle et le rapport de
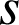 . En déduire l'écriture complexe de
. En déduire l'écriture complexe de
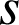 .
.
b. Calculer les affixes des points
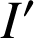 ,
,
 et
et
 images respectives de
images respectives de
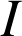 ,
,
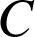 et
et
 par
par
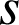 .
.
3) Pour tout point
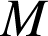 du plan, on désigne par
du plan, on désigne par
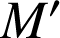 l'image de
l'image de
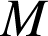 par
par
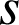 .
.
a. Quel est l'ensemble ![]() décrit par
décrit par
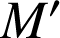 lorsque
lorsque
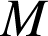 décrit
décrit ![]() ? Construire
? Construire ![]() .
.
b. Montrer que pour tout point
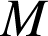 de
de ![]() , les points
, les points
 ,
,
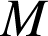 et
et
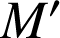 sont alignés. Construire les images des points de
sont alignés. Construire les images des points de ![]() d'abscisse
d'abscisse
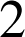 .
.
4) Soit
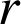 la rotation d'angle
la rotation d'angle ![]() qui transforme le point
qui transforme le point
 en
en
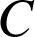 .
.
a. Construire le centre ![]() de
de
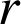 puis calculer son affixe.
puis calculer son affixe.
b. Déterminer l'image de
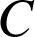 par
par ![]() . En déduire la nature et les éléments caractéristiques de
. En déduire la nature et les éléments caractéristiques de ![]() .
.
c. Écrire
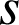 comme composée d'une homothétie suivie d'une rotation.
comme composée d'une homothétie suivie d'une rotation.
5) Soit
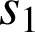 la similitude directe de centre
la similitude directe de centre
 qui transforme
qui transforme
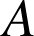 en
en
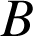 et
et
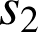 la similitude directe de centre
la similitude directe de centre
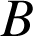 qui transforme
qui transforme
 en
en
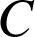 . Soit
. Soit ![]() .
.
a. Étudier la nature et préciser les éléments caractéristiques de
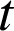 .
.
b. En utilisant l'écriture complexe de
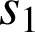 et de
et de
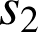 , retrouver la nature de
, retrouver la nature de
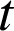 et étudier
et étudier ![]() .
.