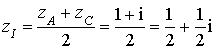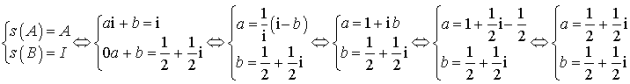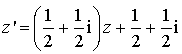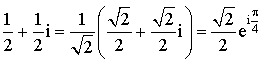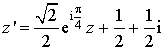Introduction
Prérequis : Cours de spécialité mathématiques sur les similitudes directes.
Durée : 90 minutes
Niveau : facile
Soit
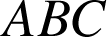 un triangle rectangle isocèle direct en
un triangle rectangle isocèle direct en
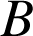 et
et
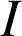 le milieu de
le milieu de ![]() .
.
1) Déterminer le rapport et l'angle de la similitude directe de centre
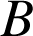 qui transforme
qui transforme
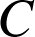 en
en
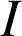 .
.
Calculer ![]() et
et ![]() .
.
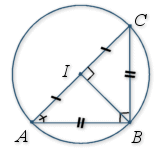
1)
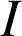 est le centre du cercle circonscrit au triangle
est le centre du cercle circonscrit au triangle
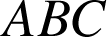 direct donc le triangle
direct donc le triangle
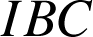 est direct.
est direct.
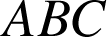 est isocèle en
est isocèle en
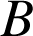 donc le triangle
donc le triangle
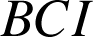 est direct et isocèle rectangle en
est direct et isocèle rectangle en
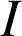 donc
donc ![]() et
et 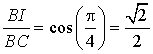 .
.
La similitude de centre
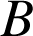 qui transforme
qui transforme
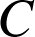 en
en
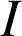 a pour rapport
a pour rapport ![]() et pour angle
et pour angle ![]() .
.
2) On rapporte le plan au repère orthonormé direct ![]() . Déterminer une écriture complexe de la similitude directe de centre
. Déterminer une écriture complexe de la similitude directe de centre
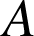 qui transforme
qui transforme
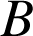 en
en
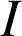 . En déduire son angle et son rapport.
. En déduire son angle et son rapport.
Déterminer les affixes des points
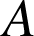 ,
,
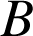 ,
,
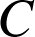 et
et
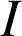 .
.
L'écriture complexe d'une similitude directe étant
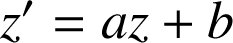 , trouver
, trouver
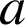 et
et
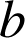 .
.
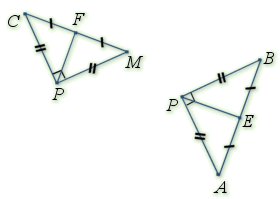
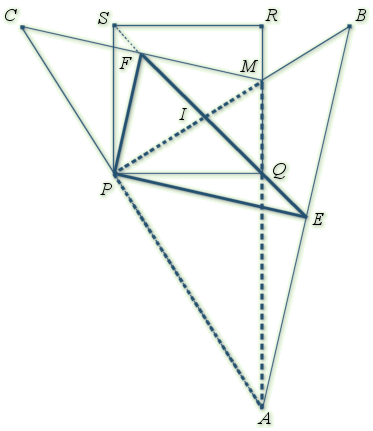
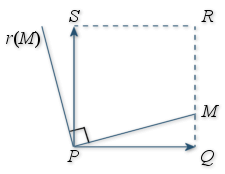
Soit
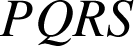 un carré de sens direct, de centre
un carré de sens direct, de centre
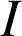 et
et
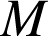 un point du segment
un point du segment ![]() distinct de
distinct de
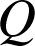 .La droite
.La droite ![]() coupe
coupe ![]() en
en
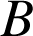 ; la perpendiculaire à
; la perpendiculaire à ![]() en
en
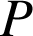 coupe
coupe ![]() en
en
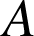 et
et ![]() en
en
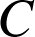 . On désigne par
. On désigne par
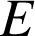 le milieu de
le milieu de ![]() et par
et par
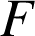 celui de
celui de ![]() .
.
1) Soit
 la rotation de centre
la rotation de centre
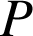 et d'angle
et d'angle ![]() .
.
a. Quelle est l'image de la droite ![]() par
par
 ?
?
b. Quelles sont les images de
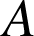 et
et
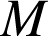 par
par
 ?
?
c. Déterminer la nature des triangles
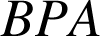 et
et
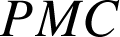 .
.
a. Quelle est l'image d'une droite par une rotation ? Quel est l'angle de
 ?
?
b. L'image de
 appartient à l'intersection des images de deux droites.
appartient à l'intersection des images de deux droites.
a. L'image de ![]() par
par
 est une droite qui passe par l'image de
est une droite qui passe par l'image de
 par
par
 .
.
b.
 appartient aux droites
appartient aux droites ![]() et
et ![]() .
.
c.
 est une isométrie .
est une isométrie .
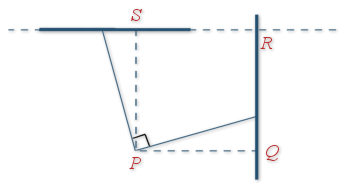
L'image de la droite ![]() par
par
 est une droite
est une droite
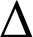 .
.
L'angle de
 est
est ![]() donc
donc
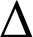 est perpendiculaire à
est perpendiculaire à ![]() .
.
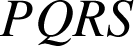 étant un carré de sens direct , l'image de
étant un carré de sens direct , l'image de
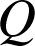 par
par
 est
est
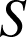 , donc
, donc
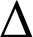 est la droite passant par
est la droite passant par
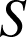 et perpendiculaire à
et perpendiculaire à ![]() qui est
qui est ![]() . L'image de
. L'image de ![]() par
par
 est
est ![]() .
.
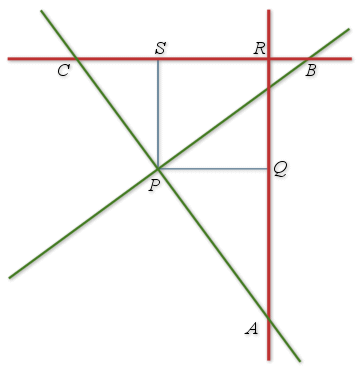
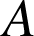 est le point d'intersection des droites
est le point d'intersection des droites ![]() et
et ![]() .
.
 transforme
transforme ![]() en
en ![]() donc l'image de
donc l'image de
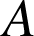 par
par
 appartient à
appartient à ![]() .
.
 transforme la droite
transforme la droite ![]() en une droite perpendiculaire à
en une droite perpendiculaire à ![]() passant par
passant par
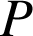 (image de
(image de
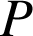 par
par
 ) c'est-à-dire en
) c'est-à-dire en ![]() .
.
L'image ![]() de
de
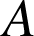 par
par
 est le point d'intersection de
est le point d'intersection de ![]() et de
et de ![]() donc :
donc : ![]() .
.
De la même façon, on détermine ![]() :
:
![]() . L'image de
. L'image de ![]() par
par
 est
est ![]() , donc
, donc ![]() appartient à
appartient à ![]() donc
donc ![]() .
.
 est la rotation de centre
est la rotation de centre
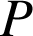 et d'angle
et d'angle ![]() .
.
![]() donc
donc ![]() et
et
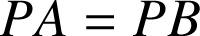 donc
donc
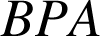 est isocèle rectangle en
est isocèle rectangle en
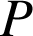 et direct.
et direct.
De même ![]() donc
donc
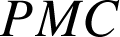 est isocèle rectangle en
est isocèle rectangle en
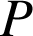 et direct.
et direct.
![]() Observez les triangles
Observez les triangles
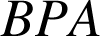 et
et
 (Java - env. 150Ko)
(Java - env. 150Ko)
2) Soit
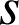 la similitude de centre
la similitude de centre
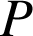 , d'angle
, d'angle ![]() et de rapport
et de rapport ![]() .
.
a. Déterminer les images par
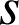 de
de
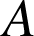 et
et
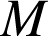 .
.
b. Quel est l'ensemble décrit par le point
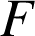 quand
quand
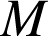 décrit
décrit ![]() privé de
privé de
 ?
?
a. Revoir les préliminaires.
b. Quelles sont les images de
 et de
et de
 par
par
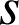 ?
?
![]() Observez le comportement de
Observez le comportement de
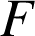 en fonction de la distance
en fonction de la distance
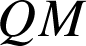 (Cabri Java - env. 150Ko)
(Cabri Java - env. 150Ko)
Dans le triangle
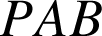 rectangle isocèle direct en
rectangle isocèle direct en
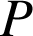 , d'après la question 1) des préliminaires,
, d'après la question 1) des préliminaires,
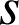 transforme
transforme
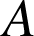 en
en
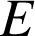 .
.
De même, dans le triangle
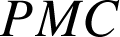 , on a
, on a ![]() .
.
Le triangle
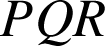 est isocèle rectangle en
est isocèle rectangle en
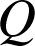 et direct donc, d'après les préliminaires :
et direct donc, d'après les préliminaires : ![]() ; de même dans le triangle
; de même dans le triangle
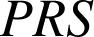 :
: ![]() .
.
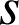 transforme le segment
transforme le segment ![]() en
en ![]() . Si
. Si
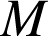 décrit
décrit ![]() privé de
privé de
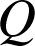 alors
alors
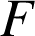 décrit privé
décrit privé ![]() de
de
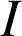 .
.
![]() Observez le comportement de
Observez le comportement de
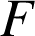 en fonction de la distance
en fonction de la distance
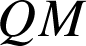 (Cabri Java - env. 150Ko)
(Cabri Java - env. 150Ko)
3) Montrer que les points
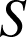 ,
,
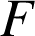 ,
,
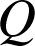 et
et
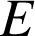 sont alignés.
sont alignés.
Quelle est l'image de la droite ![]() par
par
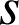 ?
?
3) Les triangles
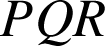 et
et
 sont isocèles rectangles et directs donc, d'après les préliminaires :
sont isocèles rectangles et directs donc, d'après les préliminaires : ![]() et
et ![]() donc
donc
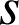 transforme
transforme ![]() en
en ![]() .
.
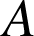 appartient à
appartient à ![]() , donc son image, qui est
, donc son image, qui est
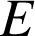 d'après la question 2.a), appartient à l'image de
d'après la question 2.a), appartient à l'image de ![]() qui est
qui est ![]() , donc
, donc ![]() , c'est-à-dire
, c'est-à-dire ![]() .
.
D'après la question précédente : ![]() donc
donc ![]() .
.
Donc les points
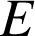 et
et
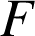 appartiennent à la droite
appartiennent à la droite ![]() .
.
![]() Observez le comportement des points
Observez le comportement des points
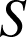 ,
,
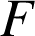 ,
,
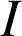 et
et
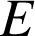 en fonction de la distance
en fonction de la distance
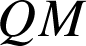 (Cabri Java - env. 150Ko)
(Cabri Java - env. 150Ko)
4) Montrer que
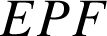 est un triangle rectangle.
est un triangle rectangle.
Le triangle
 est l'image d'un triangle par
est l'image d'un triangle par
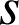 .
.
4) D'après les questions précédentes : 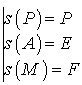 ,
,
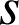 conserve les angles donc :
conserve les angles donc : ![]() .
.
Le triangle
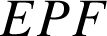 est rectangle en
est rectangle en
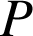 .
.
![]() Observez le comportement des triangles
Observez le comportement des triangles
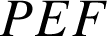 et
et
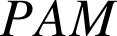 en fonction de la distance
en fonction de la distance
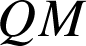 (Cabri Java - env. 150Ko)
(Cabri Java - env. 150Ko)
On se propose de retrouver, en utilisant les nombres complexes, certaines des propriétés obtenues dans la 1ère partie. On rapporte le plan au repère orthonormé direct ![]() .
.
1) Déterminer les affixes des points
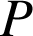 ,
,
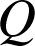 ,
,
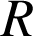 et
et
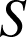 ; montrer que l'affixe de
; montrer que l'affixe de
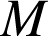 est
est ![]() où
où ![]() .
.
Les vecteurs ![]() et
et ![]() sont colinéaires.
sont colinéaires.
1) On a immédiatement : ![]() .
.
Comme ![]() alors :
alors : ![]() où
où ![]() ; donc
; donc ![]() .
.
Alors : ![]() d'où
d'où ![]() où
où ![]() .
.
2) Soit
 la rotation de centre
la rotation de centre
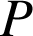 , d'angle
, d'angle ![]() . Calculer l'affixe de
. Calculer l'affixe de
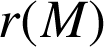 .
.
En déduire l'affixe de
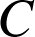 et la nature du triangle
et la nature du triangle
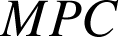 .
.
Écrire la forme complexe de
 .
.
2) L'écriture complexe de
 est
est ![]() ; l'affixe de
; l'affixe de ![]() est
est ![]() .
.
L'ordonnée est
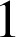 donc le point
donc le point ![]() est sur la droite
est sur la droite ![]() ; mais
; mais
 est d'angle
est d'angle ![]() ,
, ![]() appartient à la perpendiculaire en
appartient à la perpendiculaire en
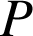 à la droite
à la droite ![]() donc :
donc : ![]() .
.
L'affixe de
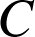 est donc
est donc ![]() et le triangle
et le triangle
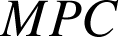 est rectangle isocèle en
est rectangle isocèle en
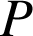 .
.
3) Calculer les affixes de
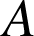 et
et
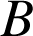 . En déduire la nature du triangle
. En déduire la nature du triangle
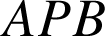 .
.
Quelle est l'abscisse de
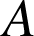 ? L'ordonnée de
? L'ordonnée de
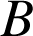 ?
?
Envisager les produits scalaires : ![]() et
et ![]() pour trouver la coordonnée manquante.
pour trouver la coordonnée manquante.
3)
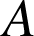 appartient à
appartient à ![]() donc son abscisse est
donc son abscisse est
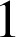 ; soit
; soit ![]() son ordonnée alors
son ordonnée alors 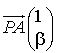 .
.
![]() donc
donc 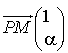 . Les droites
. Les droites ![]() et
et ![]() sont perpendiculaires donc
sont perpendiculaires donc ![]() .
.
Le repère ![]() est orthonormé donc
est orthonormé donc ![]() .
.
D'où ![]() et
et ![]() où
où ![]() .
.
De la même façon : ![]() donc
donc ![]() d'où
d'où 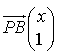 .
.
Comme 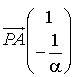 , alors :
, alors : ![]() . Donc :
. Donc : ![]() .
.
On a 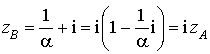 donc
donc ![]() , donc
, donc
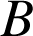 est l'image de
est l'image de
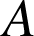 par
par
 , donc
, donc
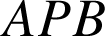 est isocèle rectangle en
est isocèle rectangle en
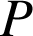 .
.
4) Déterminer une écriture complexe de
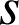 la similitude directe de centre
la similitude directe de centre
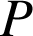 , d'angle
, d'angle ![]() , de rapport
, de rapport ![]() et montrer que
et montrer que ![]() .
.
Calculer l'affixe de l'image de
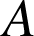 par
par
 et reconnaître l'affixe d'un milieu.
et reconnaître l'affixe d'un milieu.
4) L'écriture complexe de
 est :
est : 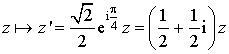 .
.
L'affixe de l'image
 par
par
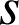 est :
est :
Donc ![]() est le milieu de
est le milieu de ![]() donc
donc ![]() .
.
5) Calculer ![]() où
où ![]() et
et ![]() sont les affixes respectives de
sont les affixes respectives de
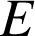 et de
et de
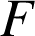 ; en déduire l'angle et le rapport de la similitude directe de centre
; en déduire l'angle et le rapport de la similitude directe de centre
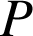 qui transforme
qui transforme
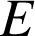 en
en
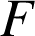 et la nature du triangle
et la nature du triangle
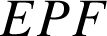 .
.
Si ![]() alors
alors
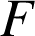 est l'image de
est l'image de
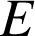 par la similitude de rapport
par la similitude de rapport ![]() et d'angle
et d'angle ![]() .
.
5) On sait que :
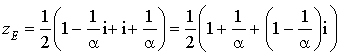
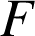 est le milieu de
est le milieu de ![]() donc :
donc :
Alors :
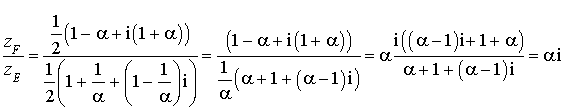
Donc ![]() et
et
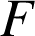 est l'image de
est l'image de
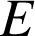 par la similitude de centre
par la similitude de centre
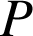 , d'angle
, d'angle ![]() et de rapport
et de rapport ![]() .
.
Le triangle
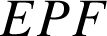 est donc rectangle en
est donc rectangle en
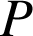 .
.
![]() Faîtes varier la distance QM et observez (Cabri Java - env. 150Ko)
Faîtes varier la distance QM et observez (Cabri Java - env. 150Ko)