Introduction
Prérequis :
Equation d'un plan de l'espace
Résolution d'équations diophantiennes
Durée : 60 minutes
Niveau : difficile
Dans l'espace muni d'un repère orthonormal ![]() , on considère
, on considère
 le plan d'équation
le plan d'équation
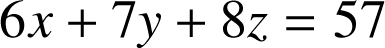 .
.
1) Montrer que les plans
 et
et ![]() sont sécants suivant une droite
sont sécants suivant une droite
 .
.
1) Un vecteur normal à
 est
est ![]() et un vecteur normal au plan
et un vecteur normal au plan ![]() est
est ![]() .
.
Ces deux vecteurs ![]() et
et ![]() ne sont pas colinéaires donc les plans ne sont pas parallèles mais sécants suivant une droite
ne sont pas colinéaires donc les plans ne sont pas parallèles mais sécants suivant une droite
 .
.
2)
a. Déterminer un couple d'entiers relatifs
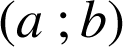 solution de l'équation
solution de l'équation
 .
.
b. Déterminer les couples d'entiers relatifs
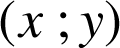 solutions de l'équation
solutions de l'équation
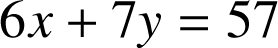 .
.
b. Revoir la méthode de résolution d'une équation diophantienne du type
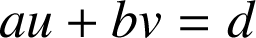 avec
avec
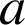 ,
,
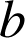 ,
,
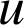 et
et
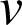 entiers et
entiers et
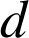
 .
.
2)
a.
 . On reconnaît ici une identité de Bézout les nombres
. On reconnaît ici une identité de Bézout les nombres
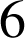 et
et
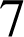 étant étrangers. Le couple
étant étrangers. Le couple
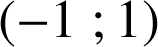 est solution de l'équation
est solution de l'équation
 .
.
b. Du a. on déduit que le couple
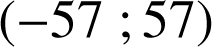 est solution de l'équation
est solution de l'équation
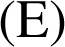
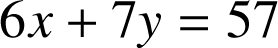 .
.
On a : 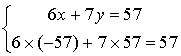 donc par soustraction membre à membre :
donc par soustraction membre à membre : ![]() soit
soit ![]() .
.
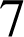 divise
divise
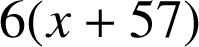 et
et
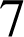 est premier avec
est premier avec
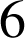 donc d'après le théorème de Gauss,
donc d'après le théorème de Gauss,
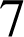 divise
divise
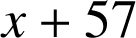 . Il existe
. Il existe
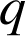 entier relatif tel que
entier relatif tel que
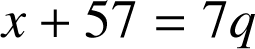 . Il est donc nécessaire que
. Il est donc nécessaire que
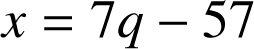 .
.
Cette condition est-elle suffisante ? Reportons dans l'équation initiale :
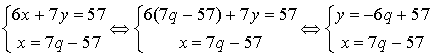
avec
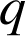 entier relatif.
entier relatif.
Les solutions entières de l'équation
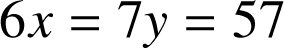 sont donc les couples
sont donc les couples
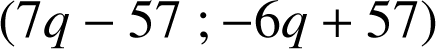 avec
avec
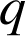 entier relatif.
entier relatif.
3) Prouver que la droite
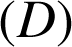 ne contient qu'un seul point dont les coordonnées sont des entiers naturels. Préciser les coordonnées de ce point.
ne contient qu'un seul point dont les coordonnées sont des entiers naturels. Préciser les coordonnées de ce point.
Trouver un système d'équations caractérisant
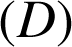 .
.
3) Une équation du plan ![]() est
est
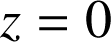 , donc les coordonnées des points de
, donc les coordonnées des points de
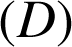 sont solutions du système :
sont solutions du système :
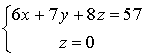 ou encore
ou encore 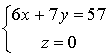
Un point
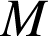 de
de
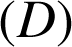 est à coordonnées entières positives si et seulement si ses coordonnées
est à coordonnées entières positives si et seulement si ses coordonnées
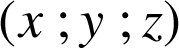 vérifient :
vérifient :
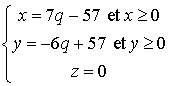 , avec
, avec
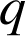 entier.
entier.
D'où avec
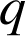 entier :
entier : ![]() .
.
De même ![]() .
.
La seule valeur de
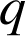 possible est
possible est
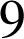 .
.
Les coordonnées du point de
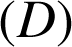 à coordonnées entières positives sont :
à coordonnées entières positives sont :
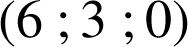 .
.
4) Qu'en est-il pour la droite
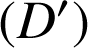 intersection des plans
intersection des plans
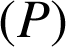 et
et ![]() ?
?
4) Le vecteur ![]() est un vecteur normal au plan
est un vecteur normal au plan ![]() . Il n'est pas colinéaire au vecteur
. Il n'est pas colinéaire au vecteur ![]() donc le plan
donc le plan ![]() et le plan
et le plan
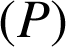 sont sécants suivant une droite
sont sécants suivant une droite
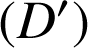 . Les coordonnées des points de
. Les coordonnées des points de
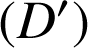 vérifient :
vérifient : 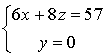 .
.
L'équation
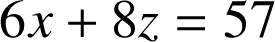 n'admet pas de couples d'entiers relatifs solutions car le
n'admet pas de couples d'entiers relatifs solutions car le
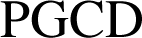 de
de
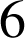 et
et
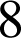 est
est
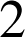 et
et
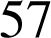 n'est pas un multiple de
n'est pas un multiple de
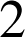 . La droite
. La droite
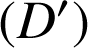 n'admet pas de points à coordonnées entières.
n'admet pas de points à coordonnées entières.
Le but de cette partie est de déterminer tous les points
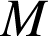 de
de
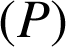 dont les coordonnées
dont les coordonnées
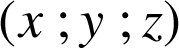 sont des entiers naturels.
sont des entiers naturels.
On suppose que de tels points existent.
1) Démontrer que
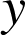 s'écrit
s'écrit
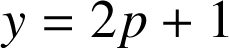 avec
avec
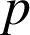 entier naturel.
entier naturel.
1) On suppose qu'il existe des entiers naturels
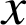 ,
,
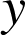 et
et
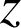 tels que
tels que
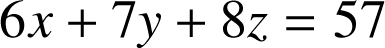 .
.
![]() .
.
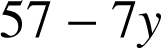 est donc un nombre pair.
est donc un nombre pair.
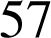 étant impair,
étant impair,
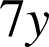 doit être impair. La seule possibilité est alors que
doit être impair. La seule possibilité est alors que
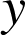 soit impair.
soit impair.
Il existe donc un entier
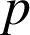 tel que
tel que
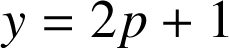 et comme
et comme
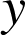 est positif,
est positif,
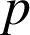 est un entier naturel.
est un entier naturel.
2) Soient
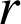 le reste de la division euclidienne de
le reste de la division euclidienne de
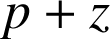 par
par
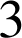 et
et
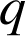 le quotient.
le quotient.
a. Montrer que
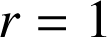 .
.
b. En déduire que
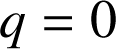 ou
ou
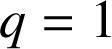 .
.
a. Penser à la définition de la division euclidienne.
b. Trouver une relation entre
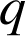 et deux des nombres
et deux des nombres
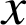 ,
,
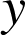 ,
,
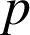 ou
ou
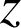 .
.
a. Penser aux différentes valeurs possibles de
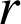 .
.
b. On peut obtenir
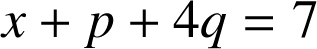 . Penser que
. Penser que
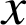 ,
,
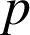 et
et
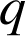 sont des entiers positifs.
sont des entiers positifs.
2)
a. On a
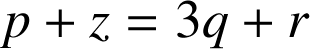 avec
avec ![]() . Remarquons que
. Remarquons que
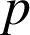 et
et
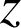 étant des entiers naturels,
étant des entiers naturels,
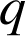 est aussi un entier naturel.
est aussi un entier naturel.
Remplaçons
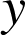 par
par
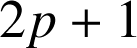 et
et
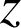 par
par
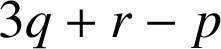 dans l'équation cartésienne de
dans l'équation cartésienne de
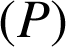 donnée.
donnée.
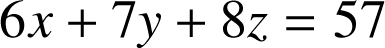 devient
devient
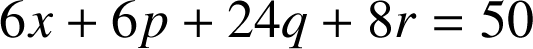 soit après simplification :
soit après simplification :
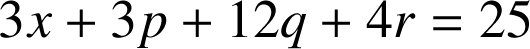 ou encore
ou encore
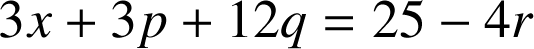 .
.
Or comme
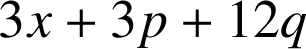 est divisible par
est divisible par
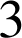 , il est nécessaire que
, il est nécessaire que
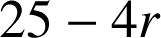 soit aussi divisible par
soit aussi divisible par
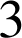 .
.
Les différentes valeurs possibles de
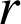 sont
sont
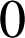 ,
,
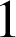 et
et
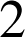 . Nous allons étudier les différents cas.
. Nous allons étudier les différents cas.
Si
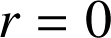 ,
,
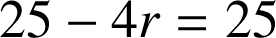 et
et
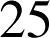 n'est pas divisible par
n'est pas divisible par
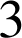 .
.Si
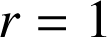 ,
,
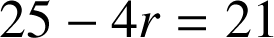 et
et
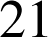 est divisible par
est divisible par
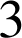 donc on ne peut exclure le cas
donc on ne peut exclure le cas
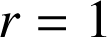 .
.Si
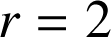 ,
,
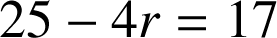 et
et
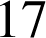 n'est pas divisible par
n'est pas divisible par
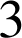 .
.
Donc
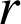 ne peut être égal qu'à
ne peut être égal qu'à
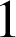 .
.
b. Avec
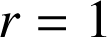 , l'équation
, l'équation
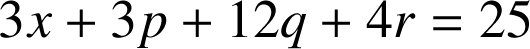 devient
devient
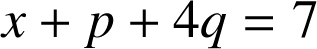 . Or
. Or
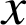 ,
,
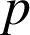 et
et
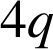 sont des entiers naturels donc ils sont tous les trois positifs et inférieurs ou égaux à
sont des entiers naturels donc ils sont tous les trois positifs et inférieurs ou égaux à
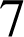 .
. ![]() avec
avec
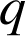 entier naturel entraîne
entier naturel entraîne
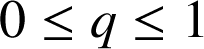 . Donc les seules valeurs possibles de
. Donc les seules valeurs possibles de
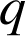 sont
sont
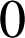 ou
ou
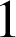 .
.
3) Conclure
Discuter suivant les valeurs de
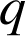 trouvées.
trouvées.
Récapitulons : nous cherchons les entiers naturels
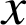 ,
,
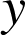 et
et
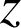 , s'ils existent, qui vérifient l'équation
, s'ils existent, qui vérifient l'équation
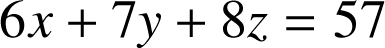 .
.
Nous avons vu qu'alors :
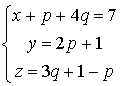 , avec
, avec
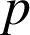 entier naturel et avec
entier naturel et avec
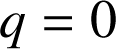 ou
ou
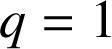 .
.
On a : 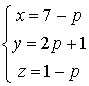 , et comme les entiers naturels
, et comme les entiers naturels
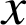 ,
,
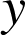 et
et
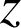 sont positifs,
sont positifs, ![]() .
.

On a : 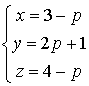 , et comme les entiers naturels
, et comme les entiers naturels
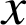 ,
,
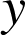 et
et
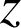 sont positifs,
sont positifs, ![]() .
.
Nous avons donc trouvé toutes les conditions nécessaires à vérifier par les entiers naturels
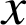 ,
,
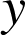 et
et
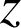 pour qu'ils puissent être solutions de l'équation
pour qu'ils puissent être solutions de l'équation
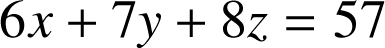 .
.
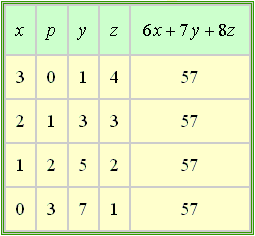
La dernière colonne des tableaux nous prouve que ces conditions sont suffisantes puisque le résultat du calcul
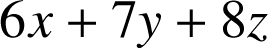 est
est
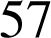 .
.
Les points de
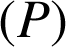 dont les coordonnées sont des entiers naturels sont donc :
dont les coordonnées sont des entiers naturels sont donc :
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.






