Introduction
Prérequis :
Congruences
Résolution d'équations diophantiennes
Durée : 90 minutes
Niveau : difficile
Objectifs :
Il s'agit d'illustrer l'emploi de quelques notions et résultats d'arithmétique en cryptographie, science qui s'occupe de chiffrer et déchiffrer des messages à l'aide d'une clé.
Nous allons travailler sur une méthode à clés cachées, c'est-à-dire que les clés ne sont connues que des personnes qui codent et décodent le message.
On assimile les lettres A, B, C, ..., Z aux nombres 0, 1, 2, ..., 25 et on code ces nombres entiers
 par
par
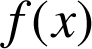 ,
,
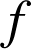 est appelée la fonction de codage, en définissant
est appelée la fonction de codage, en définissant
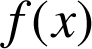 comme le reste de la division euclidienne de
comme le reste de la division euclidienne de
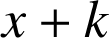 par
par
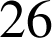 , où
, où
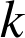 est un entier donné.
est un entier donné.
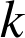 est la clé du codage.
est la clé du codage.
Prenons par exemple
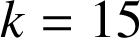 .
.
1) Coder le mot SECRET.
On affecte à chaque lettre de l'alphabet un nombre entier entre
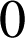 et
et
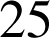 , suivant l'ordre alphabétique.
, suivant l'ordre alphabétique.
Lettre | A | B | C | ... | Z |
Nombre |
|
|
| ... |
|
La fonction de codage
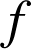 est définie par :
est définie par : ![]() avec
avec ![]() .
.
Pour coder la lettre R, assimilée au nombre
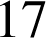 :
: ![]() donc
donc ![]() soit
soit ![]() avec
avec ![]() et finalement
et finalement ![]() donc le lettre R est codée par G.
donc le lettre R est codée par G.
1) On affecte à chaque lettre de l'alphabet un nombre entier entre
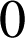 et
et
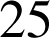 , suivant l'ordre alphabétique.
, suivant l'ordre alphabétique.
Lettre | A | B | C |
| Z |
Nombre |
|
|
|
|
|
La fonction de codage
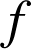 est définie par :
est définie par : ![]() avec
avec ![]() .
.
Pour coder la lettre C par exemple, on calcule
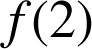 :
: ![]() avec
avec ![]() , donc
, donc
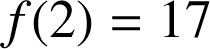 ; la lettre C est donc codée par la lettre portant le numéro 17, c'est-à-dire R.
; la lettre C est donc codée par la lettre portant le numéro 17, c'est-à-dire R.
Pour coder le lettre R, assimilée au nombre 17 : ![]() donc
donc ![]() et
et ![]() donc
donc ![]() avec
avec ![]() d'où finalement
d'où finalement
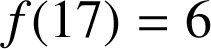 . La lettre R est codée par G.
. La lettre R est codée par G.
Lettre | A | B | C | ... | Z |
Nombre |
|
|
|
|
|
|
|
|
|
|
|
On remarque que ce codage consiste à décaler les lettres de l'alphabet de 15 rangs dans le sens de A vers Z.
Le mot SECRET se code HTRGTI.
2) Décoder le mot TJRAXST.
2) Pour décoder on décale les lettres de l'alphabet de 15 rangs dans le sens de Z vers A. Le mot TJRAXST se décode EUCLIDE.
Avec les notations de la partie A, on utilise la fonction de codage définie par : ![]() , avec
, avec ![]() . Les clés de ce codage sont
. Les clés de ce codage sont
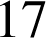 et
et
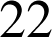 .
.
1) a. Coder le mot HUIT.
b. Montrer que si
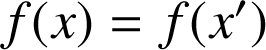 alors
alors
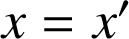 . En déduire que deux lettres distinctes ne peuvent pas être codées par la même lettre.
. En déduire que deux lettres distinctes ne peuvent pas être codées par la même lettre.
b. Utiliser les propriétés sur les congruences pour montrer que si
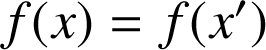 alors
alors
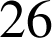 divise
divise
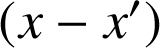 .
.
b. Montrer que si
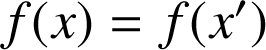 alors
alors ![]() . Remarquer que
. Remarquer que
 et
et
 sont premiers entre eux.
sont premiers entre eux.
b.
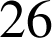 divise
divise
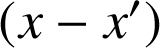 . Penser à des encadrements de
. Penser à des encadrements de
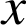 et
et
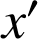 qui n'ont pas encore été utilisés.
qui n'ont pas encore été utilisés.
1) a. La lettre H est assimilée au nombre 7. ![]() avec
avec ![]() d'où
d'où
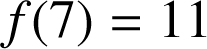 c'est-à-dire que la lettre H se code par L.
c'est-à-dire que la lettre H se code par L.
On a ainsi que le mot HUIT se code en LYCH.
1) b.
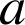 ,
,
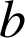 ,
,
 et
et
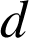 sont des entiers,
sont des entiers,
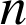 est un entier supérieur ou égal à
est un entier supérieur ou égal à
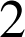 .
.
1/ si 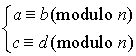 alors
alors ![]() .
.
2/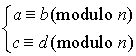 alors
alors ![]() .
.
1) b.
Si
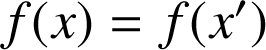 alors
alors ![]() .
.
Si
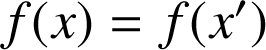 alors
alors ![]() d'après la propriété 1 sur les congruences avec
d'après la propriété 1 sur les congruences avec ![]() .
.
Si
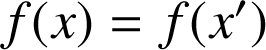 alors
alors ![]() .
.
Si
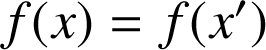 alors
alors ![]() est divisible par
est divisible par
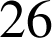 .
.
Si
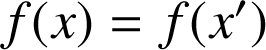 alors
alors ![]() est divisible par
est divisible par
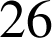 .
.
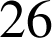 et
et
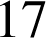 sont premiers entre eux donc d'après le théorème de Gauss,
sont premiers entre eux donc d'après le théorème de Gauss,
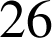 divise
divise
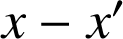 . Or
. Or ![]() et
et ![]() donc
donc 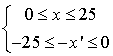 .
.
On en déduit que ![]() . Le seul multiple de
. Le seul multiple de
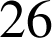 compris entre
compris entre
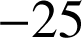 et
et
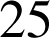 est
est
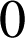 . On a donc que si
. On a donc que si
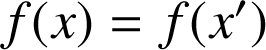 alors
alors
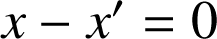 , c'est-à-dire
, c'est-à-dire
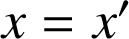 .
.
Nous devons ensuite prouver que deux lettres distinctes assimilées aux nombres
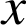 et
et
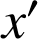 ne peuvent pas être codées par la même lettre, c'est-à-dire : si
ne peuvent pas être codées par la même lettre, c'est-à-dire : si
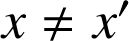 alors
alors
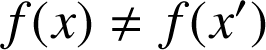 . Cette propriété est la contraposée de la proposition : si
. Cette propriété est la contraposée de la proposition : si
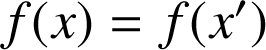 alors
alors
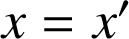 démontrée ci-dessus. Nous savons que si une proposition est vraie, sa contraposée est vraie aussi, donc ici deux lettres distinctes ne peuvent pas être codées par la même lettre. Le codage est donc un bon codage.
démontrée ci-dessus. Nous savons que si une proposition est vraie, sa contraposée est vraie aussi, donc ici deux lettres distinctes ne peuvent pas être codées par la même lettre. Le codage est donc un bon codage.
1) b. Nous avons utilisé que les nombres
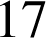 et
et
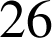 sont premiers entre eux. Cette condition est importante. Prenons la fonction de codage
sont premiers entre eux. Cette condition est importante. Prenons la fonction de codage
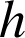 définie par
définie par ![]() , avec
, avec ![]() .
.
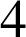 et
et
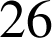 ne sont pas premiers entre eux. Un calcul rapide montre que
ne sont pas premiers entre eux. Un calcul rapide montre que
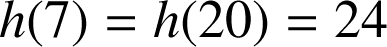 , c'est-à-dire que H et U se codent toutes les deux en Y. Cette fonction de codage ne peut donc pas être utilisée.
, c'est-à-dire que H et U se codent toutes les deux en Y. Cette fonction de codage ne peut donc pas être utilisée.
2) Pour pouvoir décoder un message, nous allons définir une fonction de décodage.
a. Déterminer un entier
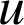 tel que
tel que ![]() .
.
b. En déduire l'expression d'une fonction de décodage
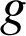 telle que : si
telle que : si
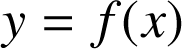 alors
alors
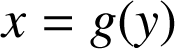 .
.
c. Déchiffrer le mot NMFAYH.
a. ![]()
![]() « il existe
« il existe
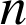 entier tel que
entier tel que
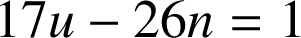 ».
».
b. Soit
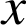 le nombre codé en
le nombre codé en
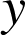 .
. ![]() .
.
Utiliser les propriétés sur les congruences pour isoler
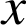 .
.
a. Pour trouver une solution particulière de l'équation
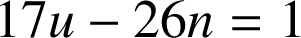 , écrire l'algorithme d'Euclide pour la recherche du
, écrire l'algorithme d'Euclide pour la recherche du
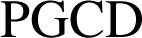 de
de
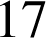 et
et
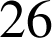 .
.
b. ![]() et
et ![]() donc
donc ![]() .
.
Utiliser ensuite que ![]() .
.
2) a. ![]()
![]() «
«
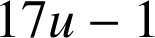 est divisible par
est divisible par
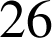 ».
».
![]()
![]() « il existe
« il existe ![]() tel que
tel que
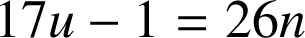 ».
».
Il suffit donc de trouver un entier
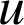 tel que
tel que
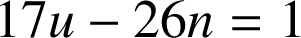 .
.
On reconnaît une identité de Bézout car
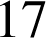 et
et
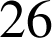 sont premiers entre eux, on sait donc que cette équation a des solutions entières. Pour trouver une solution particulière nous allons écrire l'algorithme d'Euclide pour la recherche du
sont premiers entre eux, on sait donc que cette équation a des solutions entières. Pour trouver une solution particulière nous allons écrire l'algorithme d'Euclide pour la recherche du
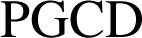 de
de
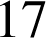 et
et
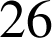 , puis « remonter » cet algorithme pour arriver à une solution particulière.
, puis « remonter » cet algorithme pour arriver à une solution particulière.
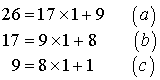
Le dernier reste
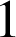 est le
est le
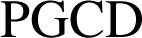 de
de
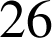 et
et
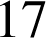 .
.
Partons de (
 ) :
) :
 .
.
De (
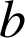 ) l'on tire
) l'on tire
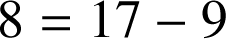 que l'on reporte dans (
que l'on reporte dans (
 ) :
) : ![]() .
.
De (
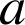 ) l'on tire
) l'on tire
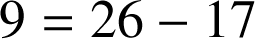 que l'on reporte dans (
que l'on reporte dans (
 ) :
) : ![]() , soit
, soit ![]() . Une solution particulière de l'équation
. Une solution particulière de l'équation
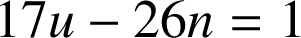 est donc
est donc
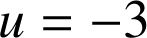 et
et
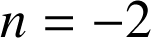 .
.
Nous prendrons
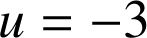 (remarque :
(remarque :
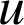 peut prendre une infinité de valeurs, toutes celles solutions de l'équation
peut prendre une infinité de valeurs, toutes celles solutions de l'équation
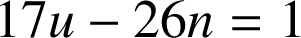 ).
).
b. Il s'agit maintenant de décoder une lettre correspondant au nombre
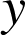 avec
avec ![]() . On cherche donc
. On cherche donc
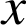 tel que :
tel que : ![]() et
et
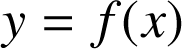 soit
soit ![]() .
.
![]() donc
donc ![]() .
.
Utilisons
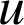 et
et ![]() .
.
On a ![]() et
et ![]() , donc d'après la propriété 2 sur les congruences
, donc d'après la propriété 2 sur les congruences ![]() , soit encore
, soit encore ![]() d'où
d'où ![]() (encore la propriété 2 avec
(encore la propriété 2 avec ![]() et
et ![]() ).
).
Donc si
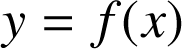 alors
alors
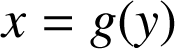 avec
avec ![]() où
où
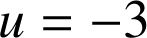 et
et ![]() .
.
c. Pour décoder la lettre N assimilée au nombre
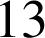 on calcule
on calcule
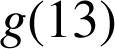 .
.
![]() soit
soit ![]() d'où
d'où ![]() et
et ![]() donc
donc
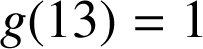 .
.
N est donc la lettre codée B. Le mot NMFAYH se décode BEZOUT.