Introduction
Prérequis :
Nombres premiers
Décomposition en produit de facteurs premiers
Durée : 50 minutes
Niveau : facile
On appelle nombre parfait tout entier naturel
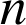 dont la somme des diviseurs positifs est égale à
dont la somme des diviseurs positifs est égale à
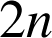 .
.
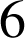 est un nombre parfait car
est un nombre parfait car ![]() .
.
A1)
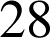 est-il un nombre parfait ?
est-il un nombre parfait ?
Les diviseurs positifs de
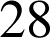 sont
sont
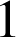 ,
,
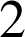 ,
,
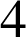 ,
,
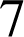 ,
,
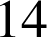 et
et
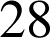 .
.
![]() , donc
, donc
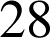 est un nombre parfait.
est un nombre parfait.
A2) Euclide a énoncé la règle suivante : « Si un nombre
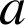 s'écrit
s'écrit ![]() et si le facteur
et si le facteur ![]() est premier, alors
est premier, alors
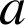 est un nombre parfait ». On se propose de démontrer ce théorème.
est un nombre parfait ». On se propose de démontrer ce théorème.
Posons ![]() avec
avec ![]() premier.
premier.
a. Quelle est la décomposition de
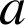 en produit de facteurs premiers ?
en produit de facteurs premiers ?
b. En déduire la liste des diviseurs positifs de
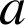 . Combien y en a t-il ?
. Combien y en a t-il ?
c. Démontrer que
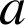 est parfait.
est parfait.
Il existe une réciproque de ce théorème due à Léonard Euler (1707-1783) :
« Tout nombre parfait pair s'écrit ![]() avec
avec ![]() premier ». La démonstration est trop compliquée pour être présentée ici. Le problème de savoir s'il existe des nombres parfaits impairs n'est toujours pas résolu.
premier ». La démonstration est trop compliquée pour être présentée ici. Le problème de savoir s'il existe des nombres parfaits impairs n'est toujours pas résolu.
b. Revoir le cours sur la décomposition d'un entier en produit de facteurs premiers.
c. Repérer dans la somme les termes indépendants de
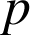 .
.
Penser à la somme des premiers termes d'une suite géométrique.
a. Nous avons ![]() avec
avec ![]() premier. Nous remarquons qu'alors
premier. Nous remarquons qu'alors
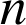 est différent de
est différent de
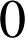 . En effet
. En effet ![]() est égal à
est égal à
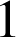 si et seulement si
si et seulement si
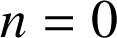 et
et
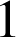 n'est pas un nombre premier.
n'est pas un nombre premier.
Pour
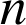 strictement positif,
strictement positif,
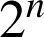 est différent de
est différent de
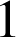 .
.
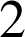 est un nombre premier et
est un nombre premier et ![]() aussi par hypothèse donc la décomposition de
aussi par hypothèse donc la décomposition de
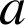 en produit de facteurs premiers est
en produit de facteurs premiers est ![]() .
.
b. Soit
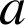 un entier dont la décomposition en produit de facteurs premiers est :
un entier dont la décomposition en produit de facteurs premiers est : ![]() où
où ![]() sont des nombres premiers,
sont des nombres premiers, ![]() sont des entiers strictement positifs. Alors les diviseurs positifs de
sont des entiers strictement positifs. Alors les diviseurs positifs de
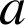 sont les nombres :
sont les nombres : ![]() avec pour tout
avec pour tout
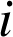 entier tel que
entier tel que ![]() ,
, ![]() .
.
b. Les nombres premiers
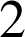 et
et ![]() sont respectivement élevés dans la décomposition de
sont respectivement élevés dans la décomposition de
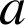 à la puissance
à la puissance
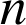 et
et
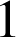 . Les diviseurs positifs de
. Les diviseurs positifs de
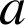 sont les nombres
sont les nombres ![]() , soit
, soit
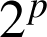 ,
, ![]() et
et ![]() avec
avec ![]() . Il y a
. Il y a
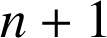 façons de choisir l'exposant dans
façons de choisir l'exposant dans
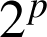 et pour chacune de ces façons il y a 2 façons de choisir l'exposant de
et pour chacune de ces façons il y a 2 façons de choisir l'exposant de ![]() , (exposant
, (exposant
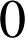 ou
ou
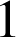 ). Il y a donc
). Il y a donc
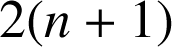 diviseurs positifs de
diviseurs positifs de
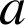 .
.
c. Soit
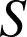 la somme des diviseurs positifs de
la somme des diviseurs positifs de
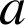 .
.
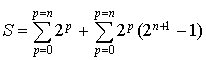
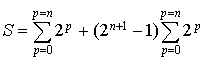 car le nombre
car le nombre ![]() ne dépend pas de
ne dépend pas de
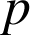 ; il est donc constant et peut être mis en facteur dans la seconde somme.
; il est donc constant et peut être mis en facteur dans la seconde somme.
On peut encore factoriser
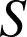 et obtenir
et obtenir 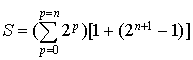 soit
soit 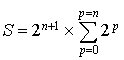 .
.
Calculons ![]() . Nous reconnaissons la somme des
. Nous reconnaissons la somme des
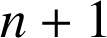 premiers termes de la suite géométrique des puissances de
premiers termes de la suite géométrique des puissances de
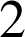 .
. 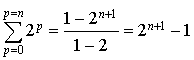 .
.
D'où ![]() , soit
, soit ![]() . On reconnaît à l'intérieur des crochets le nombre
. On reconnaît à l'intérieur des crochets le nombre
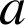 donc
donc
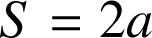 . Le nombre
. Le nombre
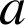 est bien un nombre parfait.
est bien un nombre parfait.
![]() et
et ![]() .
.
Nous avons prouvé dans la partie A que les nombres ![]() où
où ![]() est premier, sont parfaits. Est-il simple de trouver ces nombres
est premier, sont parfaits. Est-il simple de trouver ces nombres ![]() premiers ?
premiers ?
Le mathématicien français Marin Mersenne (1588-1648) affirme que les nombres ![]() sont premiers pour certaines valeurs de
sont premiers pour certaines valeurs de
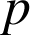 :
:
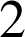 ,
,
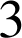 ,
,
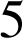 ,
,
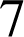 ,
,
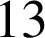 ,
,
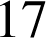 ,
,
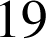 ,
,
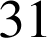 ,
,
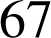 ,
,
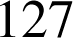 ,
,
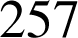 . Il fait une erreur pour
. Il fait une erreur pour
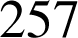 et oublie des valeurs. A l'heure actuelle il est prouvé que
et oublie des valeurs. A l'heure actuelle il est prouvé que ![]() est premier pour
est premier pour
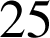 valeurs de
valeurs de
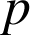 inférieures ou égales à
inférieures ou égales à
 .
.
Nous allons prouver que : si ![]() est premier alors
est premier alors
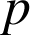 est premier.
est premier.
B1) Montrer que pour tout
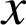 réel et
réel et
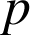 entier naturel non nul :
entier naturel non nul : ![]() .
.
Calculer ![]() pour
pour
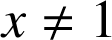 .
.
Pour
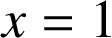 l'égalité est vérifiée car
l'égalité est vérifiée car
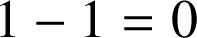 donc le premier membre de l'égalité est nul et
donc le premier membre de l'égalité est nul et
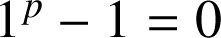 donc le second membre est nul lui aussi, d'où l'égalité.
donc le second membre est nul lui aussi, d'où l'égalité.
Pour
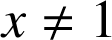 ,
, ![]() est la somme des
est la somme des
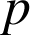 premiers termes de la suite géométrique des puissances de
premiers termes de la suite géométrique des puissances de
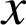 . On a
. On a ![]() d'où
d'où ![]() .
.
Cette factorisation de
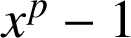 est à retenir. Elle est souvent utilisée.
est à retenir. Elle est souvent utilisée.
B2) Démontrer que ![]() où
où
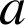 et
et
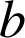 sont des entiers naturels non nuls est divisible par
sont des entiers naturels non nuls est divisible par ![]() .
.
Utiliser la factorisation de l'expression de la question B1)
D'après les propriétés sur les puissances ![]() .
.
Appliquons la propriété de la question 1) en posant : ![]() et
et
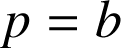 .
.
Il vient : ![]() .
.
![]() et
et ![]() sont des nombres entiers non nuls (
sont des nombres entiers non nuls (
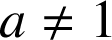 ), donc
), donc ![]() est divisible par
est divisible par ![]() .
.
B3) Conclure.
Soit
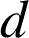 un diviseur positif de
un diviseur positif de
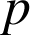 . Déterminer les valeurs possibles de
. Déterminer les valeurs possibles de
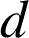 .
.
D'après la question B2), ![]() divise
divise ![]() .
.
Nous allons montrer la proposition : si ![]() est premier alors
est premier alors
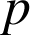 est premier.
est premier.
Soit
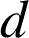 un diviseur positif de
un diviseur positif de
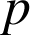 .
.
D'après la propriété de la question 2), ![]() est un diviseur positif de
est un diviseur positif de ![]() .
.
Or ![]() est un nombre premier donc
est un nombre premier donc ![]() ou
ou ![]() .
.
La première égalité donne
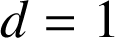 et la deuxième
et la deuxième
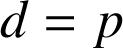 . Les seuls diviseurs positifs de
. Les seuls diviseurs positifs de
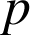 sont
sont
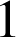 et
et
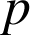 , donc
, donc
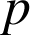 est un nombre premier.
est un nombre premier.
Nous avons montré que si ![]() est premier alors
est premier alors
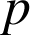 est premier.
est premier.
Remarquons que la réciproque de cette propriété est fausse.
La réciproque est : Si
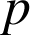 est premier alors
est premier alors ![]() est premier. Prenons
est premier. Prenons
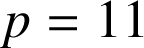 ,
,
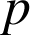 est premier or
est premier or ![]() n'est pas premier.
n'est pas premier.






