Ecoulement à potentiel des vitesses
Rappels
Hypothèses : on se place dans le cas d'un fluide parfait incompressible en écoulement plan irrotationnel et permanent.
Dans ce cas, la vitesse dérive du potentiel
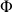
Et l'équation de continuité s'écrit :
Pour connaître l'écoulement (ligne de courant, vitesse), il faut donc résoudre l'équation de Laplace. pour les écoulements à deux dimensions, la méthode des potentiels complexes, décrites ci-dessous, est très fructueuse.
Conditions de Cauchy - Riemann
Soit f(z) la fonction de la variable complexe x + i y, f(z) est dérivable sur un domaine D si, dans le plan complexe :
On peut mettre f(z) sous la forme :
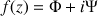
Où
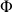est la fonction potentielle et
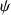la fonction courant
Calcul de la dérivée
Pour que f soit analytique (
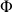et
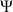satisfont à l'équation de Laplace), cette dérivée doit être indépendante de dz, soit, en développant :
Fonction holomorphe
La condition d'indépendance implique que
On obtient donc les relations :
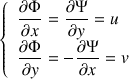
u et v sont les composantes de la vitesse
Ce sont les conditions de Cauchy Riemann
On dit que la fonction f(z) est holomorphe sur le domaine D
EXERCICE
Trouver les lignes de courant et les équipotentielles dans les cas suivants :
Le potentiel complexe est : f(z) = V.z où V est une constante réelle et Z = x +i y
Le potentiel complexe est : f(z) = k ln(z) où k est une constante réelle
