Champ des vitesses
Cas du solide parfait (indéformable) - rappels
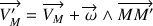
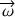est le vecteur rotation et :
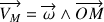
En calculant
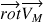, on peut écrire
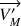sous la forme
Interprétation physique
Le premier terme de l'expression de la vitesse représente une translation et le deuxième une rotation du solide.
Le terme 1 /2
où
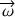est le vecteur rotation.
Cas du fluide – Vecteur tourbillon et tenseur des taux de déformation
Soit un élément de volume dt et deux points M et M' infiniment voisins. Dans le repère O, x, y, z les coordonnées de M et M' sont :
M(x, y, z) et M'(x+dx, y+dy, z+dz)
Expression de la vitesse
Les coordonnées de la vitesse sont :
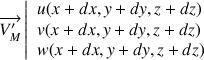
Nous allons simplement exprimer les coordonnées de la vitesse en M' en utilisant la formule des accroissements finis. Par exemple pour la composante suivant x :
vi représente une composante de la vitesse au point M'
Sous forme vectorielle, on peut écrire
Pour comparer l'expression précédente avec celle du fluide parfait et mettre en évidence la signification des différents termes, développons et calculons
On obtient donc :
Tenseur des taux de déformation
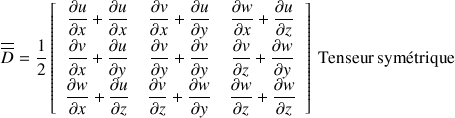
Pour mettre en évidence la signification physique des différents termes, écrivons la vitesse sous la forme :
Remarque : si
, le taux de déformation est nul et l'on se ramène au cas du solide parfait indéformable (ou au cas d'un milieu déformable en équilibre absolu relatif)
Voyons le sens physique des différents termes
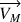: Représente une translation d'ensemble de l'élément de volume
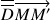représente la déformation de l'élément de volume
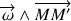: est le moment par rapport à M' du vecteur 1/2
; c'est la répartition des vitesses lors d'une rotation en bloc de l'élément de volume autour d'un axe passant par M
Mouvement de fluide : translation + rotation + déformation
