Accélération
Expression de l'accélération
Soit
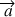le vecteur accélération, par définition, on a :
Dans le repère considéré,
a les coordonnées :
Prenons la coordonnée de la vitesse suivant l'axe x et calculons sa différentielle :
Cette expression permet de calculer la composante de l'accélération sur l'axe x :
Forme vectorielle
On peut écrire l'expression précédente :
On peut écrire le même type de relation pour les composantes suivant y et z, on obtient donc une relation vectorielle :
Autre écriture
En utilisant une égalité vectorielle, on obtient :
Interprétation physique :
est appelé accélération locale, ce terme traduit la non permanence de l'écoulement, il est nul pour un écoulement permanent
Accélération convective
est l'accélération convective, ce terme traduit la non uniformité de l'écoulement.
Pour vérifier si un écoulement est permanent, on se place en un point fixe de l'écoulement et on mesure la vitesse à des instants différents.
Pour voir si un écoulement est uniforme, on mesure la vitesse en différents points de l'écoulement, au même instant.
