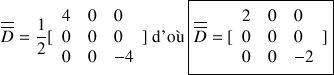Problème classique
On considère un écoulement permanent défini dans un repère (0, x, y, z) par le champs des vitesses suivant, en variables d'Euler :

Question
1) Montrer que le fluide est incompressible.
2) Calculer le champs des vecteurs accélération
 .
.
3) Déterminer les équations du réseau des lignes de courant.
4) Déterminer le champs des tenseurs des taux de déformation.
1) Il suffit de montrer que

2) L'accélération, d'après le cours, est définie par
3) Les lignes de courant sont définies par l'équation :

4) Il vous suffit de consulter votre cours...
1) Montrer que le fluide est incompressible.
Nous devons montrer que
 .
.
Il nous suffit de vérifier que l'équation suivante est vraie :

Après un rapide calcul nous obtenons :
 ;
;
 ;
;

La somme de ces 3 termes vaut zéro, le fluide est bien incompressible.
2) Calculer le champs des vecteurs accélération
L'accélération est définie par :
L'écoulement est permanent d'où
 et donc
et donc

Après calcul nous obtenons :


3) Déterminer les équations du réseau des lignes de courant.
Les lignes de courant sont définies par :

Nous avons v=0. Pour que cette équation soit définie, il faut que dy=0. L'écoulement se situe dans le plan Oxz.
Nous allions transformer cette équation...

Ce qui nous donne

Puis

Enfin
4) Déterminer le champs des tenseurs des taux de déformation.
Par définition le tenseur des taux de déformation est donné par :

Après simplification et un rapide calcul, on obtient :