Ecoulement de Couette
Hypothèses
ne autre situation simple est celle de l'écoulement de Couette. On a les mêmes hypothèses que précédemment sur la géométrie du conduit, sur le fluide et l'écoulement. La différence vient du fait que la paroi supérieure possède une vitesse V. Comme dans l'exemple précédent, on néglige les forces de pesanteur. On obtient bien sûr la même équation différentielle avec des conditions aux limites qui changent.
Les conditions aux limites deviennent : u(b) = V et u(-b) = 0.
Solutions
La solution générale de l'équation est (comme dans l'exemple précédent) :
Avec les conditions aux limites, on trouve K et K' :
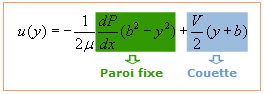
La solution s'écrit donc :
Profil des vitesses
On peut écrire le profil des vitesses sous la forme :
On pose :
K1 apparaît comme un gradient de pression adimensionnel.
K1 > 0 le gradient de pression décroissant est dans le sens du mouvement donc u[[yes]] est toujours positif.
K1 < 0 et inférieur à –1/2 la vitesse devient négative au voisinage de la paroi (le sens de l'écoulement est inversé).
A titre d'exercice, étudier les différents cas possibles et faire un schéma des différents profils de vitesses obtenus.





