Ecoulement dans un conduit bidimensionnel
Hypothèses
On considère un conduit bidimensionnel infini, d'épaisseur 2b faible, l'axe x coïncide avec l'axe de symétrie du conduit.
Le fluide est considéré comme newtonien, incompressible en écoulement stationnaire (permanent) selon l'axe x.
On choisit un repère cartésien, la projection de l'équation de Navier Stokes donne :
Symétrie : dans tout plan xOy, on a le même profil donc w = 0
Il n'y a pas de composantes de la vitesse suivant y donc v = 0
L'équation de continuité div
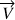= 0 impose
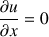
Équation différentielle
Solution
Détermination du gradient de pression
Le gradient de pression peut être évalué, en effet si on néglige les forces de pesanteur :
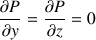donc
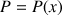
On peut donc écrire en appelant P1 et P2 les pressions à l'entrée et à la sortie de la conduite :
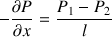l est la longueur de la conduite, P1 >P2.
Il suffit de mesurer les pressions correspondantes pour déterminer le gradient de pression.
Définition : Vitesse moyenne de l'écoulement
La vitesse moyenne de l'écoulement est définie par :
S : section du conduit,
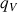: débit en volume
Le débit en masse par unité d'aire :
Pour le conduit bidimensionnel, on trouve :
La vitesse maximale :
La vitesse moyenne :
Le débit en masse par unité d'aire :
