Deuxième problème de Stokes
On considère un fluide incompressible de viscosité dynamique μ, de masse volumique ρ au dessus d'une plaque plane d'étendue infinie. Cette plaque effectue un mouvement oscillatoire dans son propre plan. A cause de la viscosité du fluide, des oscillations longitudinales sont engendrées dans le fluide au dessus de la plaque.
Dans ce cas, la vitesse d'un point M du fluide n'a qu'une composante u suivant l'axe x et cette composante ne dépend que de z et du temps t (u = u(z,t)) où z est l'axe vertical dans un repère d'inertie.
Les conditions aux limites sont les suivantes :
pour z = 0, u(0,t) = Uexp(iωt) où U est l'amplitude de la vitesse de la plaque et ω la pulsation des oscillations.
pour
Question
1 - Déterminer l'équation différentielle à laquelle obéit la vitesse u(z,t). On posera ν = μ/ρ où ν est la viscosité cinématique.
2 - Trouver la solution de cette équation. Pour ce faire, on procédera par la méthode de séparation des variables en posant :
U(z,t) = f(t).g(z)
où f(t) est une fonction ne dépendant que de t et de g(z) une fonction ne dépendant que de z.
3 - En notant que
calculer la distance caractéristique δ pour laquelle l'amplitude est amortie à 1/e de sa valeur en z = 0.
4 - Le déplacement longitudinal qu'effectue la plaque est donnée par :
a - Calculer le rapport δ/L.
b - Quelle est la signification de ce rapport ?
1 - Ecrire les équations de Navier Stokes. Attention! L'écoulement est non permanent.
2 - Pour qu'il existe une solution, il faut que les deux équations différentielles (en f et en g) soient égales à une constante k.
Attention! Il ne faut pas oublier les conditions aux limites.
1 - Déterminer l'équation différentielle à laquelle obéit la vitesse u(z,t).
On écrit l'équation de Navier Stokes dans le cas présent :
Après quelques calculs on obtient :
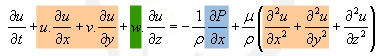
Les termes en couleur sont nuls :
u ne dépend que de z et t.
Le mouvement est oscillatoire suivant x.
V n'a pas de composante verticale.
On obtient donc :
2 - Trouver la solution de cette équation
On pose U(z,t) = f(t).g(z). On peut alors écrire notre équation :
Ce qui nous donne les solutions suivantes :
Avec la condition à la paroi
, on obtient :
3 - Calculer la distance caractéristique δ pour laquelle l'amplitude est amortie à 1/e de sa valeur en z = 0.
On remarque que :
On obtient alors :
On a donc un mouvement oscillatoire du fluide au dessus de la plaque (amorti avec la distance par rapport à la plaque).
On vérifie que pour
, l'amplitude est amortie à
de sa valeur en z=0.
4 a - Calculer le rapport δ/L.
Le calcul est simple.
4 b - Quelle est la signification de ce rapport ?
On a donc
.L'effet de la viscosité est limité à une couche d'épaisseur relative inversement proportionnelle à la racine carrée de R.
