Exo 7
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère le plan affine euclidien
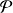 de repère orthonormé
de repère orthonormé
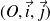 .
.
Question
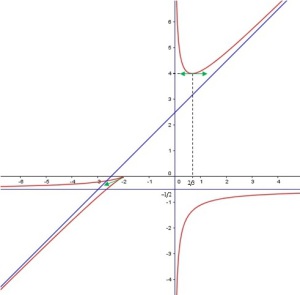
Construire la courbe
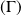 de représentation paramétrique :
de représentation paramétrique :
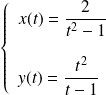 .
.
La fonction
 est définie sur
est définie sur
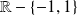 et elle est paire.
et elle est paire.
La fonction
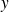 est définie sur
est définie sur
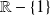 et n'est ni paire ni impaire.
et n'est ni paire ni impaire.
Donc la représentation paramétrique est définie sur
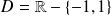 .
.
On ne peut pas réduire l'étude.
Etude lorsque t tend vers l'infini
A l'infini :
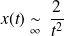 et
et
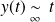 . Donc :
. Donc :
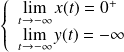 et
et
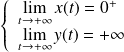 .
.
Donc la courbe
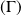 admet une asymptote verticale d'équation
admet une asymptote verticale d'équation
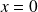 .
.
Etude lorsque t tend vers (-1)
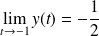 , et :
, et :
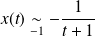 . Donc :
. Donc :
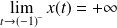 et
et
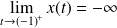 .
.
Donc la courbe
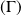 admet une asymptote horizontale d'équation
admet une asymptote horizontale d'équation
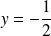 .
.
Et :
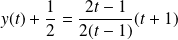 , donc :
, donc :
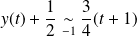 .
.
Donc, lorsque
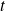 tend vers
tend vers
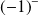 , la courbe est en dessous de l'asymptote, et lorsque
, la courbe est en dessous de l'asymptote, et lorsque
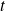 tend vers
tend vers
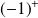 , la courbe est au dessus de l'asymptote.
, la courbe est au dessus de l'asymptote.
Etude lorsque t tend vers 1
Il y a une branche infinie car :
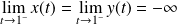 et :
et :
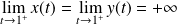 .
.
Donc on calcule :
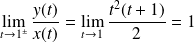 .
.
Et :
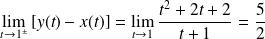 .
.
Donc la courbe admet une asymptote oblique d'équation :
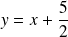 .
.
De plus :
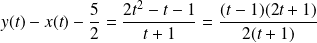 . Donc :
. Donc :
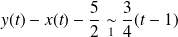 .
.
Donc, lorsque
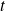 tend vers
tend vers
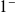 , la courbe est en dessous de l'asymptote, et lorsque t tend vers
, la courbe est en dessous de l'asymptote, et lorsque t tend vers
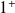 , la courbe est au dessus de l'asymptote.
, la courbe est au dessus de l'asymptote.
Etude des variations
Les fonctions
 et
et
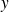 sont de classe
sont de classe
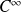 sur
sur
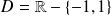 .
.
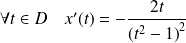 . Donc :
. Donc :
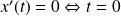 et
et
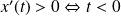 .
.
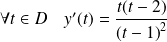 . Donc :
. Donc :
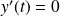 si et seulement si
si et seulement si
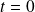 ou
ou
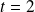 .
.
Et :
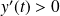 si et seulement si
si et seulement si
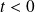 ou
ou
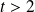 .
.
Etude du point de paramètre 0
Le point de paramètre
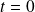 est un point singulier car
est un point singulier car
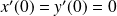 .
.
Pour étudier la nature de ce point, il faut trouver les deux premières dérivées non nulles.
On remarque que :
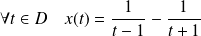 , et
, et
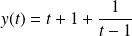 .
.
Donc, si
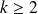 :
:
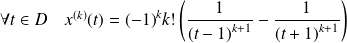 , et
, et
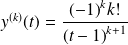 .
.
Donc :
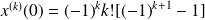 , et
, et
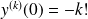 pour tout
pour tout
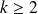 .
.
Donc les deux premiers vecteurs dérivés non nuls sont d'ordre
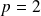 et
et
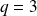 .
.
Donc le point de paramètre
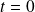 est un point de rebroussement de première espèce.
est un point de rebroussement de première espèce.
Et, au point de paramètre
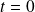 , la tangente a pour vecteur directeur
, la tangente a pour vecteur directeur
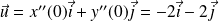 .
.
Tableau de variations
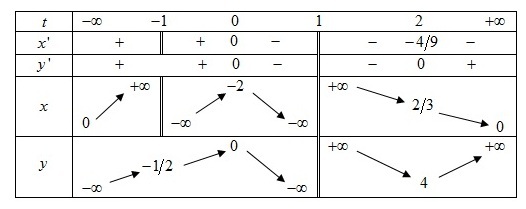
Courbe
|