Exo 4
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère le plan affine euclidien
 de repère orthonormé
de repère orthonormé
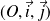 .
.
Question
Construire la courbe
 de représentation paramétrique :
de représentation paramétrique :
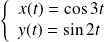 .
.
Les fonctions
 et
et
 sont définies sur
sont définies sur
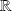 .
.
Réduction de l'étude
La fonction
 est périodique de période
est périodique de période
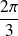 et la fonction
et la fonction
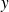 de période
de période
 .
.Donc :
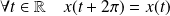 et :
et :
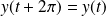 .
.Donc on réduit l'étude à un intervalle de longueur
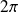 , par exemple
, par exemple
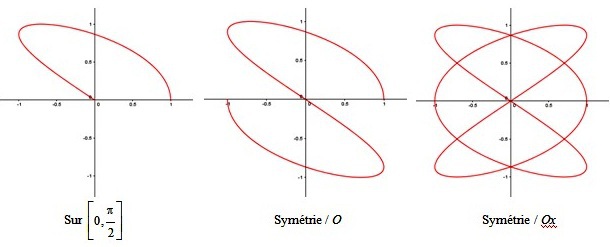
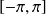 . On obtiendra ainsi toute la courbe.
. On obtiendra ainsi toute la courbe.De plus :
 et :
et :
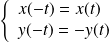 .
.Donc on réduit l'étude à l'intervalle
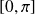 et on complètera la courbe par symétrie par rapport à l'axe des abscisses.
et on complètera la courbe par symétrie par rapport à l'axe des abscisses.De plus :
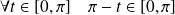 et :
et :
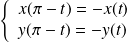 .
.Donc on réduit l'étude à l'intervalle
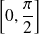 et on complètera la courbe par symétrie par rapport au point
et on complètera la courbe par symétrie par rapport au point
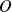 .
.
Etude des variations
Les fonctions
 et
et
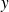 sont de classe
sont de classe
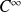 sur
sur
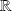 , donc sur
, donc sur
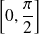 .
.
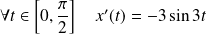 . Or :
. Or :
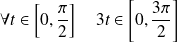 .
.
Donc :
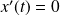 si et seulement si
si et seulement si
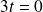 ou
ou
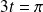 , donc si
, donc si
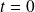 ou
ou
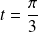 .
.
Et :
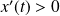 si et seulement si
si et seulement si
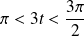 , donc si
, donc si
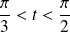 .
.
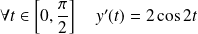 . Or :
. Or :
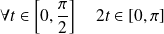 .
.
Donc :
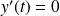 si et seulement si
si et seulement si
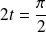 , donc si
, donc si
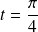 .
.
Et :
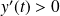 si et seulement si
si et seulement si
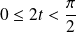 , donc si
, donc si
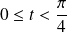 .
.
Tableau de variations
Tous les points sont réguliers puisque
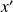 et
et
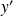 ne s'annulent pas simultanément.
ne s'annulent pas simultanément.
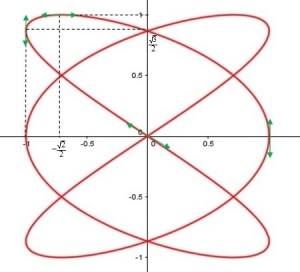
Courbe
On complète ensuite la courbe d'abord par symétrie par rapport au point
|