Etude d'une courbe plane en représentation paramétrique cartésienne
On suppose que le plan affine euclidien
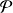est rapporté à un repère orthonormal
.
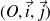Définition :
Une courbe plane en représentation paramétrique cartésienne est définie par la donnée d'un intervalle
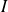et de deux fonctions
et
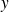de classe
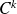de
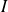dans
.
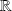Les points de
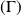sont définis par :
.
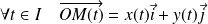Exemple : Soit
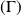la courbe de représentation paramétrique
.
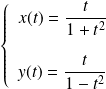Cette représentation paramétrique est définie lorsque le paramètre
décrit
.
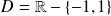Fondamental :
Réduction de l'intervalle d'étude
S'il existe un réel
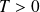tel que
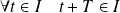et
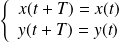, alors on réduit l'étude à un intervalle de longueur
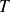et on obtient ainsi toute la courbe.S'il existe un intervalle
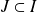et une application
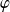injective de
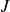dans
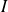telle que
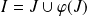, et si
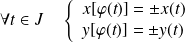, alors on réduit l'étude à l'intervalle
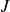et on complète la courbe :par symétrie par rapport à l'axe
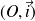si :
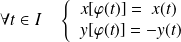.par symétrie par rapport à l'axe
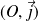si :
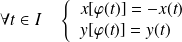.par symétrie par rapport au point
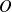si :
.
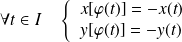Dans l'exemple précédent, on peut remarquer que
est symétrique par rapport à
et que :
.
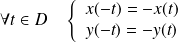Donc on peut réduire l'étude à
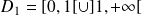et compléter la courbe
par symétrie par rapport au point
.
On peut aussi remarquer que lorsque le paramètre
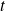décrit
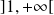, alors
décrit l'intervalle
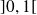et que :
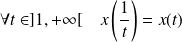et
.
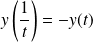Donc on peut réduire l'étude à
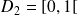et compléter la courbe
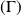par symétrie par rapport à l'axe des abscisses.
Fondamental :
Etude asymptotique
Soit
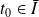(donc éventuellement
) .
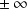Si
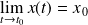et
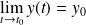, alors la courbe admet un "point limite"
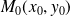, avec une tangente de pente
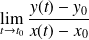.Si
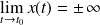et
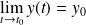, alors la courbe admet une asymptote horizontale d'équation
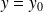.Si
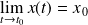et
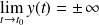, alors la courbe admet une asymptote verticale d'équation
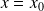.Si
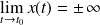et
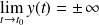, alors on étudie
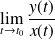:Si
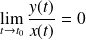, alors la courbe admet une branche parabolique de direction
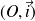.Si
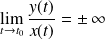, alors la courbe admet une branche parabolique de direction
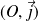.Si
(
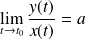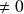) et
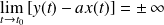, alors la courbe admet une direction asymptotique
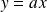.Si
(
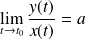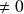) et
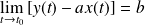, alors la courbe admet une asymptote oblique d'équation
.
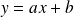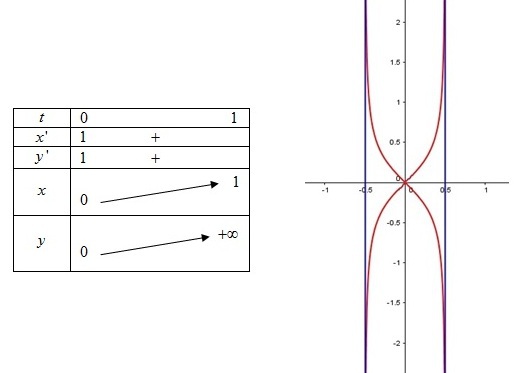
Dans l'exemple précédent, on a une branche infinie lorsque
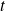tend vers
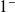car
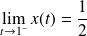et
.
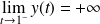Donc la courbe
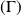admet une asymptote verticale d'équation :
.
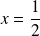Méthode :
L'étude comparée des variations des fonctions
et
permet de tracer la courbe
.
Dans l'exemple précédent, on construit un tableau regroupant les variations de
et de
, ce qui permet de tracer la courbe.
Pour certains points, on est amené à faire une étude locale, en particulier lorsque les fonctions
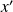et
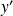s'annulent simultanément.
Fondamental :
Etude locale
Sous réserve d'existence, soit
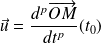où
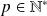est le plus petit entier pour lequel
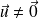. Alors la courbe admet au point
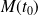une tangente de vecteur directeur
.
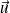Sous réserve d'existence, soit
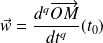où
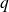le plus petit entier strictement supérieur à
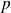pour lequel
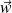n'est pas colinéaire à
.
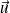La forme de la courbe au voisinage du point
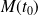est déterminée par la parité de
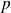et
.
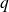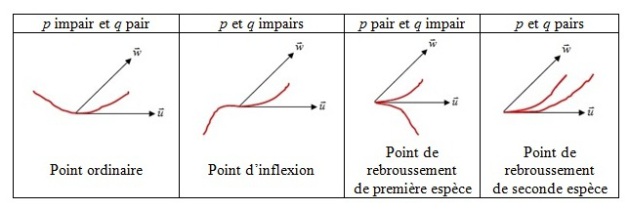
Lorsque le point
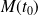est birégulier, on a
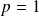et
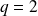, donc un point ordinaire.
Fondamental :
En prenant pour origine le point
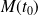, l'abscisse curviligne d'un point
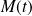est :
.
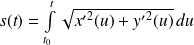La courbure de la courbe au point
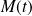est :
.
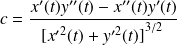