Quelques exemples classiques d'équations non linéaires
Voici quelques exemples d'équations non linéaires pour lesquelles on connaît une méthode de résolution.
Dans la suite, la variable sera notée
 car on effectue parfois un paramétrage en
car on effectue parfois un paramétrage en
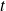 .
.
Définition :
Une équation différentielle à variables séparables d'ordre
 est une équation de la forme :
est une équation de la forme :
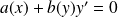 où
où
 et
et
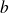 sont des fonctions continues.
sont des fonctions continues.
Méthode : On intègre séparément chaque terme. On obtient une équation cartésienne des courbes intégrales.
Exemple : Résoudre l'équation différentielle
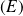 :
:
 .
.
Définition :
Une équation de Bernoulli est une équation de la forme :
 où
où
 et
et
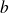 sont des fonctions continues et où
sont des fonctions continues et où
 est un réel différent de
est un réel différent de
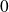 et de
et de
 .
.
Méthode : On effectue un changement de fonction :
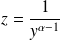 .
.
Exemple : Résoudre l'équation différentielle
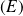 :
:
 .
.
Définition :
Une équation de Ricatti est une équation de la forme :
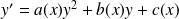 où
où
 ,
,
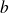 et
et
 sont des fonctions continues.
sont des fonctions continues.
Méthode : Si
 est une solution particulière,
est une solution particulière,
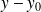 vérifie une équation de Bernoulli.
vérifie une équation de Bernoulli.
Exemple : Résoudre l'équation différentielle
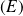 :
:
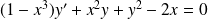 .
.
Définition :
Une équation de Lagrange est une équation de la forme :
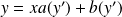 .
.
Méthode : On paramètre les courbes intégrales en posant
 : on exprime
: on exprime
 et
et
 en fonction de
en fonction de
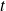 .
.
Exemple : Résoudre l'équation différentielle
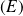 :
:
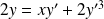 .
.
Définition :
Une équation homogène est une équation de la forme :
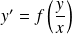 .
.
Méthode : On paramètre les courbes intégrales en posant
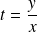 : on exprime
: on exprime
 et
et
 en fonction de
en fonction de
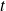 .
.
Exemple : Résoudre l'équation différentielle
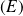 :
:
 .
.





