Equation de Ricatti
Exemple :
Résoudre l'équation différentielle
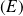 :
:
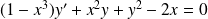 .
.
On peut remarquer que la fonction
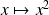 est solution.
est solution.
On pose :
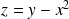 , donc :
, donc :
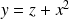 et :
et :
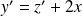 .
.
Donc
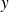 est solution de l'équation
est solution de l'équation
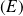 si et seulement si :
si et seulement si :
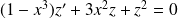 .
.
On obtient une équation de Bernoulli que l'on résout sur
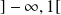 et sur
et sur
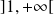 .
.
La fonction nulle est solution sur chacun de ces intervalles, et pour tout réel
 , c'est la seule solution maximale qui s'annule en
, c'est la seule solution maximale qui s'annule en
 .
.
Donc les solutions maximales non constantes ne s'annulent pas. Donc on pose :
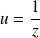 .
.
Donc
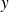 est solution de l'équation
est solution de l'équation
 si et seulement si :
si et seulement si :
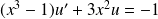 .
.
Le premier membre est la dérivée de
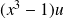 .
.
Donc :
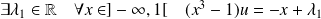 , donc
, donc
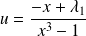 .
.
Et :
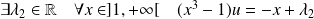 , donc
, donc
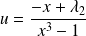 .
.
Or :
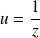 . Donc la fonction
. Donc la fonction
 ne s'annule pas. Il faut donc que :
ne s'annule pas. Il faut donc que :
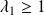 et
et
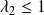 .
.
On en déduit les solutions de
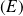 car :
car :
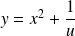 .
.
Sur l'intervalle
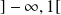 :
:
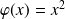 ou
ou
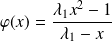 avec
avec
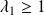 .
.Si
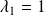 , on obtient :
, on obtient :
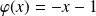 .
.
Sur l'intervalle
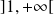 :
:
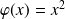 ou
ou
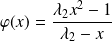 avec
avec
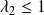 .
.Si
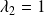 , on obtient :
, on obtient :
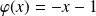 .
.
Les solutions sur
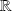 sont continues et dérivables en
sont continues et dérivables en
 .
.
Si :
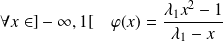 avec
avec
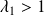 , alors :
, alors :
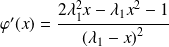 .
.
Donc :
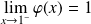 et
et
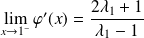 , donc
, donc
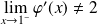 et
et
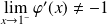 .
.
Donc on ne peut raccorder ni avec
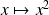 ni avec
ni avec
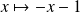 .
.
Et on ne peut pas raccorder non plus avec
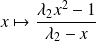 pour
pour
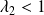 car il faudrait que
car il faudrait que
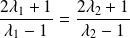 , donc que
, donc que
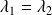 ce qui n'est pas possible si
ce qui n'est pas possible si
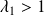 et
et
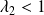 .
.
Donc les seules solutions de l'équation
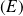 sur
sur
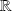 sont :
sont :
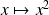 et
et
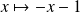 .
.
