Equation de Bernoulli

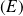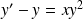La fonction constante nulle est solution de l'équation .

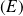Or d'après le théorème de Cauchy-Lipschitz, pour tout réel , il existe une unique solution maximale 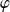qui vérifie 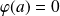 : la solution nulle.

Donc les solutions maximales non constantes ne s'annulent pas.

On pose : 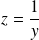. Donc : .

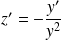Donc 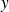est solution de l'équation 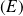si et seulement si : .

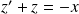On obtient une équation linéaire qui a pour solution particulière la fonction .

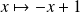L'équation homogène associée : 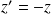a pour solutions les fonctions .

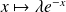Donc 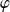est solution de l'équation 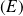si et seulement si il existe un réel 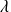tel que : .

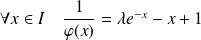Il faut donc que : .

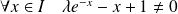Conclusion : Les solutions de l'équation 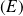sont la fonction nulle et les fonctions 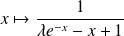où .
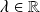