Equation de Lagrange
Exemple :
Résoudre l'équation différentielle
:
.
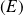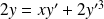On prend comme nouvelle variable :
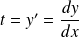. Donc :
.
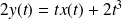On dérive par rapport à
:
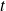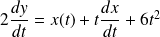. Or :
.
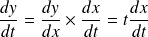Donc :
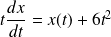. Donc la fonction
est solution de l'équation :
.
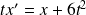Il s'agit d'une équation linéaire du premier ordre.
La fonction
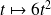est solution particulière de cette équation.
Et l'équation homogène associée
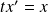a pour solutions
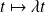avec
.
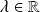Donc :
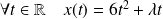et :
.
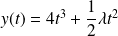On obtient une représentation paramétrique des courbes intégrales.
