Equation homogène

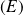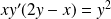Il s'agit d'une équation homogène car elle peut s'écrire : .

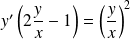On se place sur 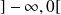ou 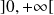et l'on prend comme nouvelle variable : .

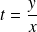L'équation devient : 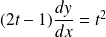. Or : 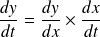. Donc : .

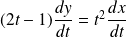Or : 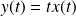, donc : .

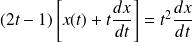Donc la fonction est solution de l'équation : .

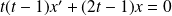Si 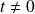et 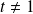: 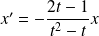. Une primitive de 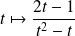est : .

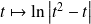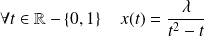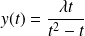Donc : et avec .

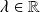On obtient une représentation paramétrique des courbes intégrales.

Le cas 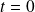correspond à 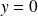. Effectivement, la fonction nulle est solution de l'équation .

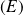Le cas 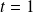correspond à 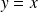. Effectivement, la fonction 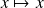est aussi solution de l'équation .

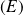Une équation cartésienne de toutes les courbes intégrales est : 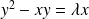où .
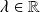