Equation à variables séparables
Exemple :
Résoudre l'équation différentielle
:
.
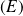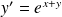L'équation
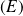équivaut à :
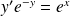. Il s'agit donc d'une équation à variables séparables.
Une fonction
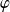est solution sur un intervalle
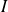si et seulement si il existe une constante
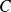telle que :
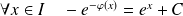, donc telle que :
.
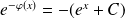La constante
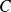doit donc être strictement négative. Soit :
.
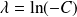Donc :
.
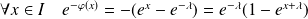Alors :
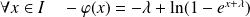, donc :
.
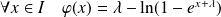Il faut donc que :
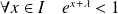, donc que :
, donc que :
.
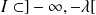Réciproquement, sur
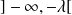, la fonction
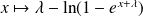est solution de
.
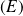Donc les solutions maximales de
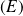sont les fonctions
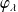définies sur
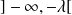par
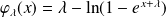pour tout
.
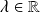