Exo 10
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les questions suivantes sont indépendantes.
Soit
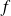la fonction définie par :
.
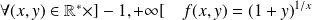Question
Montrer que la fonction
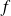n'admet pas de limite en
.
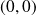Construisez deux suites qui tendent vers
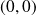, mais dont les images n'ont pas la même limite.
Remarque :
Il s'agit encore de fonctions de
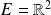dans
.
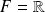L'espace vectoriel
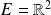étant de dimension finie, on peut choisir n'importe quelle norme, par exemple :
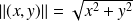. Et sur
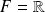, on utilise la valeur absolue.
On a :
.
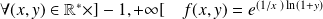Si
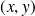tend vers
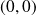, alors
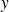tend vers
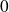, donc
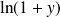est équivalent à
.
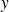Donc
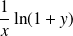est équivalent à
.
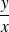Donc, pour démontrer que
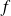n'a pas de limite, il suffit de construire deux suites qui tendent vers
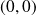, mais pour lesquelles
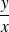n'a pas la même limite.
Par exemple :
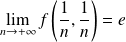et :
.
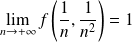Conclusion : La fonction
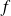n'admet pas de limite en
.
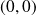Soit
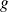la fonction définie par :
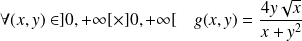et :
.
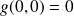Question
Montrer que la fonction
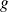n'est pas continue en
.
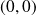Construisez une suite qui tend vers
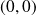, mais dont l'image par
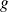ne tend pas vers
.
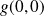Pour démontrer que
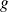n'est pas continue en
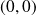, il suffit de construire une suite qui tend vers
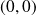, mais dont l'image par
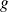ne tend pas vers
.
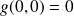On remarque par exemple que :
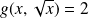, donc :
.
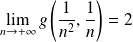Conclusion : La fonction
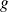n'est pas continue en
.
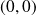