Limite et continuité d'une fonction dans un espace vectoriel normé
Dans ce qui suit,
et
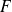désignent deux espaces vectoriels normés dont les normes sont notées
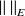et
.
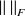Un élément
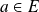est adhérent à une partie
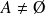de
si :
.
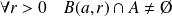Définition :
Soit
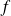une application d'une partie
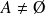de
dans
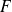et
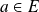un point adhérent à
.
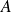L'application
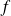admet en
une limite
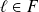si :
.
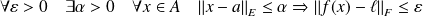Dans le cas où
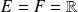, on retrouve la définition usuelle d'une limite.
Fondamental :
Propriétés :
La limite, si elle existe, est unique et on la note :
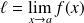ou
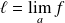.Si une fonction admet en
une limite
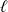pour une norme, elle admet la même limite
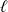pour toute norme équivalente.L'ensemble des fonctions définies sur
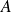et qui admettent une limite en
est un espace vectoriel et l'application qui à toute fonction associe sa limite est linéaire.Une application
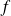admet en
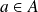une limite
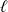si et seulement si, pour toute suite
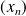d'éléments de
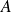qui converge vers
, la suite
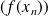converge vers
.
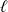Donc, s'il existe deux suites
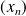et
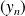d'éléments de
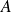qui convergent vers
telles que les suites
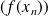et
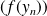n'admettent pas la même limite, alors la fonction
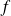n'admet pas de limite en
.
Définition :
Une application
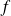d'une partie
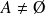de
dans
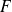est continue en
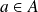si elle admet en
une limite. Alors :
.
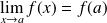Les propriétés sont conséquences des propriétés des limites.
Fondamental :
Propriétés :
Si une fonction est continue en
pour une norme, elle est continue en
pour toute norme équivalente.L'ensemble des fonctions définies sur
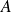et continues en
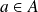est un espace vectoriel.Une application
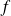est continue en
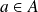si et seulement si, pour toute suite
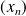d'éléments de
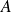qui converge vers
, la suite
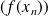converge vers
.
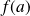Donc pour démontrer qu'une fonction
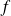n'est pas continue en
, il suffit de trouver une suite
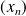d'éléments de
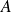qui converge vers
telle que la suite
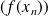ne converge pas vers
.
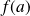Définition :
Une application
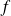d'une partie
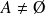de
dans
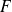est continue sur
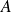si elle est continue en tout point de
.
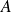Par exemple, l'application
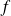de
dans
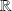définie par
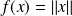est continue sur
.
Soit
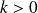. Une application
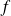de
dans
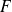est
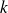- lipschitzienne si :
.
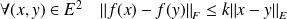Fondamental :
Toute application
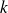- lipschitzienne de
dans
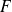est continue sur
.
Dans le cas des applications linéaires :
.
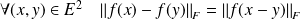Fondamental :
Cas des applications linéaires
Une application linéaire de
dans
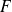est continue sur
si et seulement si elle est continue en
:
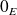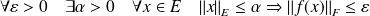.Une application linéaire
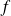de
dans
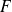est continue sur
si et seulement si elle est bornée sur la boule unité
:
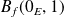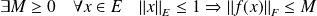.Si
est de dimension finie, toute application linéaire de
dans
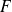est continue sur
.
En particulier, si
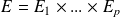est un produit d'espaces vectoriels normés, les applications composantes
:
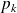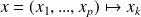sont continues sur
muni de la norme produit.
Définition :
L'application qui à toute application
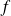linéaire de
dans
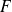et continue sur
associe le réel
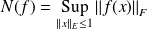est une norme sur l'espace vectoriel des applications linéaires continues sur
, appelée norme subordonnée aux normes de
et de
.
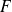Fondamental :
Propriétés :
Une autre expression de la norme subordonnée est :
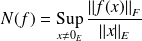.Si
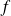et
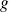sont linéaires et continues, alors :
.
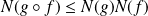