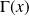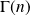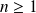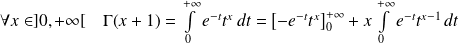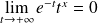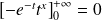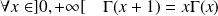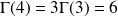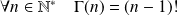Exo 13
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
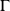la fonction définie par :
.
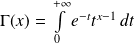Question
Déterminer l'ensemble de définition
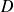de la fonction
.
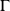Déterminez pour quelles valeurs de
l'intégrale converge.
Soit
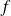la fonction définie par :
.
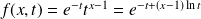Pour tout réel
, la fonction
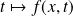est continue sur
.
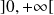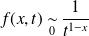, donc l'intégrale
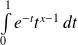converge si et seulement si
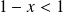, donc si
.
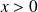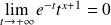, donc :
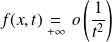, donc l'intégrale
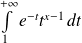converge.
Conclusion : L'ensemble de définition de la fonction
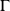est
.
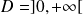Question
Question
Démontrer que la fonction
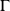est de classe
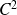sur
.
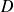Utilisez une domination locale.
Les fonctions
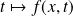et
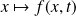sont continues et positives sur
.
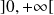Soit
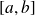un segment inclus dans
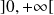et soit
.
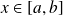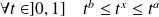, donc :
.
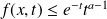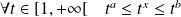, donc :
.
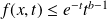Donc :
où
.
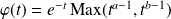La fonction
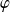est continue par morceaux sur
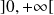et intégrable sur
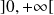d'après la première question car
.
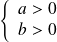Donc, par domination locale, la fonction
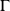est continue sur
.
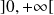La fonction
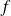admet une dérivée partielle d'ordre
:
.
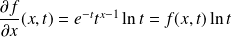Donc les fonctions
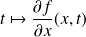et
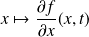sont continues sur
.
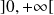Et si
:
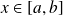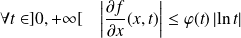où
.
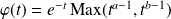La fonction
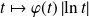est continue par morceaux sur
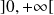et intégrable sur
.
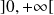Donc, par domination locale, la fonction
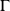est de classe
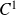sur
.
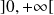Et :
.
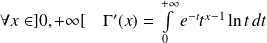Le raisonnement est le même à l'ordre
.
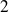La fonction
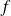admet une dérivée partielle d'ordre
:
.
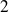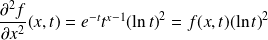Donc les fonctions
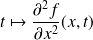et
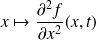sont continues et positives sur
.
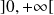Et si
:
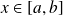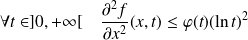où
.
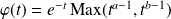La fonction
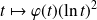est continue par morceaux sur
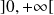et intégrable sur
.
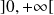Donc, par domination locale, la fonction
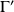est de classe
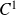sur
.
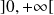Et :
.
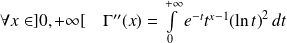Conclusion : La fonction
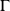est de classe
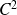sur
.
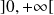Question
En déduire l'étude des variations de la fonction
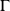sur
.
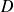Etudiez le sens de variations de la fonction
.
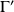La fonction
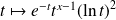est continue et positive sur
.
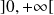Elle n'est pas identiquement nulle. Donc :
.
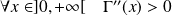Donc la fonction
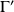est strictement croissante sur
.
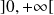Elle s'annule donc au plus une fois sur
.
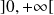Or :
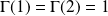, donc d'après le théorème de Rolle, la fonction
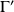s'annule au moins une fois entre
et
.
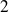Conclusion : L'équation
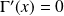admet une unique solution
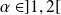, et la fonction
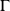est décroissante sur
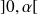et croissante sur
.
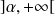Question
Etudier les limites de la fonction
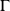aux bornes de
.
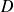En
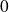, utilisez l'expression de
.
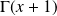En
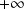, utilisez la partie entière de
.
Par continuité de la fonction
:
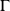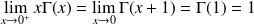, donc :
.
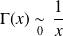Conclusion :
.
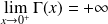La courbe de la fonction
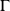admet une asymptote verticale d'équation
.
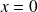Par croissance de la fonction
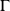sur
:
.
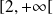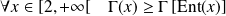Donc :
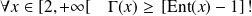
Conclusion :
.
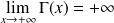Question
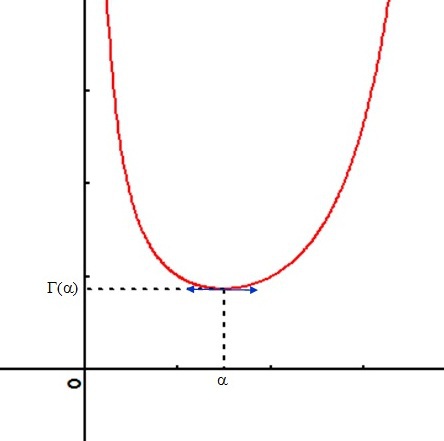
En déduire l'allure de sa courbe représentative.
Le tableau de variations de la fonction
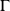est de la forme suivante :
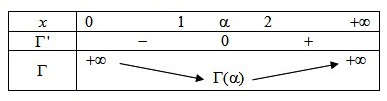
Comme
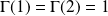, on sait que :
.
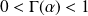On peut démontrer que
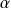est voisin de
et que
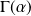est voisin de
.
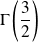Or :
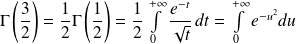en posant
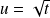, donc
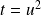et
.
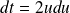On retrouve l'intégrale de Gauss, déjà étudiée. Donc :
.
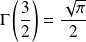Pour tracer la courbe, on utilisera :
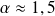et
.
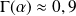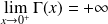, donc la courbe admet une asymptote verticale d'équation
.
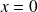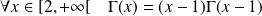. Or :
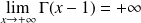, donc :
.
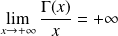Donc la courbe admet en
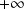une branche parabolique de direction
.
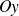