Exo 11
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Etudier la fonction
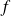définie par :
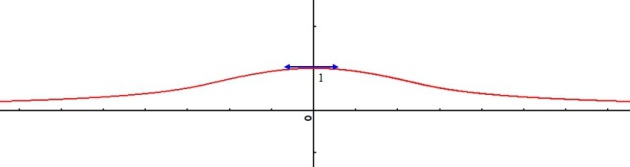
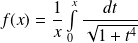et donner l'allure de sa courbe représentative.
Introduisez une primitive de la fonction
.
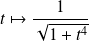Pour l'étude des variations, exprimez
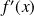en fonction de
.
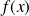Pour l'étude en
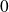, utilisez des développements limités.
Pour l'étude en
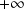, comparez
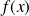et
.
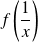La fonction
:
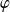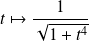est continue sur
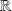, donc admet une unique primitive
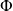qui s'annule en
.
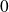Et :
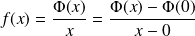, donc :
.
Donc la fonction
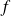est définie, continue sur
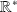, et prolongeable par continuité en
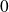en posant
.
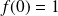Réduction de l'étude :
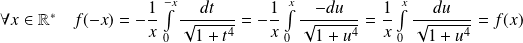en posant
.
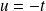Donc la fonction
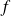est paire. Il suffit donc de l'étudier en
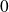et sur
.
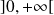La courbe sera ensuite complétée par symétrie par rapport à l'axe des ordonnées.
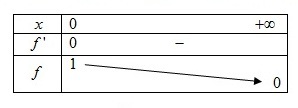
Etude des variations :
La fonction
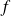est dérivable sur
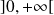comme quotient de fonctions dérivables.
.
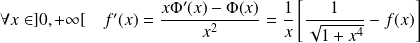Or :
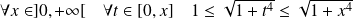, donc
.
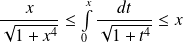Donc :
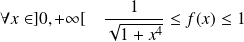, donc :
.
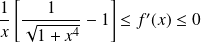Donc la fonction
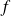est décroissante sur
.
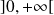Etude en
:
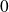Au voisinage de
:
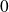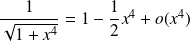, donc :
.
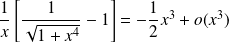Donc :
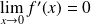et le prolongement par continuité de
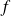est dérivable en
:
.
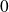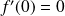Etude en
:
.
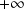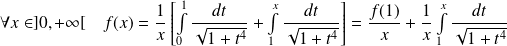Dans l'intégrale, on pose :
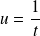, donc :
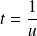et
.
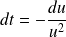Donc :
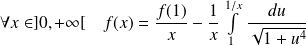. Or :
.
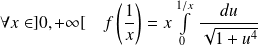Donc :
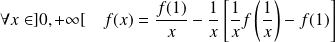, donc :
.
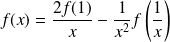Or :
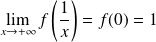. Donc :
.
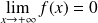La courbe de
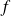admet en
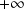une asymptote horizontale d'équation
.
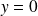