Exo 10
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
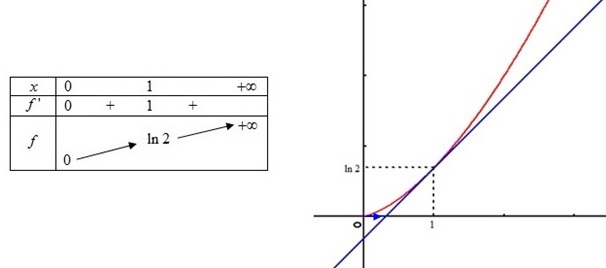
Etudier la fonction
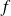 définie par :
définie par :
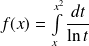 et donner l'allure de sa courbe représentative.
et donner l'allure de sa courbe représentative.
Etudiez la continuité de la fonction :
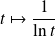 pour trouver l'ensemble de définition de
pour trouver l'ensemble de définition de
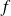 .
.
Utilisez des encadrements pour trouver les limites de la fonction
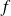 .
.
La fonction
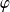 :
:
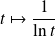 est continue sur
est continue sur
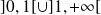 .
.
Donc la fonction
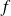 est définie si :
est définie si :
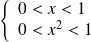 ou
ou
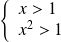 , donc sur
, donc sur
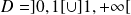 .
.
Etude des variations :
Les fonctions
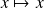 et
et
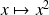 sont dérivables sur
sont dérivables sur
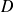 .
.
Donc la fonction
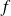 est dérivable sur
est dérivable sur
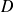 .
.
Soit
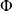 une primitive de
une primitive de
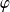 sur
sur
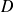 :
:
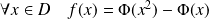 .
.
Donc :
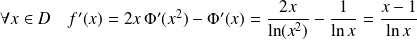 .
.
Or le signe de
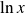 est le même que celui de
est le même que celui de
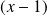 . Donc :
. Donc :
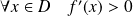 .
.
Donc la fonction
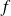 est strictement croissante sur
est strictement croissante sur
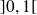 et sur
et sur
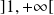 .
.
Etude en
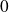 :
:
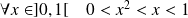 , et :
, et :
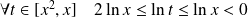 .
.
Donc :
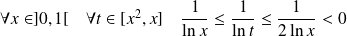 .
.
Donc :
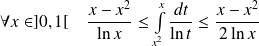 , donc :
, donc :
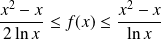 .
.
Or :
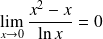 , donc :
, donc :
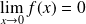 .
.
Donc la fonction
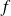 est prolongeable par continuité en
est prolongeable par continuité en
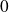 en posant :
en posant :
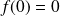 .
.
Et :
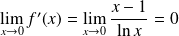 . Donc le prolongement est dérivable en
. Donc le prolongement est dérivable en
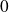 :
:
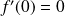 .
.
Etude en
 :
:
Par concavité :
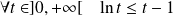 , donc
, donc
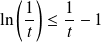 .
.
Donc :
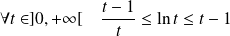 . Ces trois termes sont de même signe.
. Ces trois termes sont de même signe.
Donc :
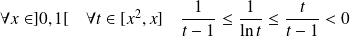 . Et :
. Et :
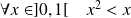 .
.
Donc :
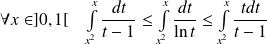 , donc :
, donc :
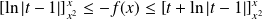 .
.
Donc :
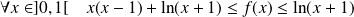 . Donc :
. Donc :
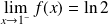 .
.
De même :
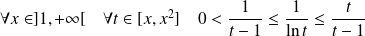 . Et :
. Et :
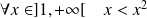 .
.
Donc :
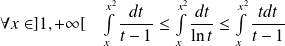 , donc :
, donc :
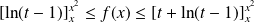 .
.
Donc :
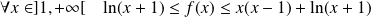 . Donc :
. Donc :
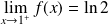 .
.
Donc la fonction
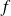 est prolongeable par continuité en
est prolongeable par continuité en
 en posant :
en posant :
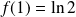 .
.
Et :
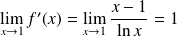 . Donc le prolongement est dérivable en
. Donc le prolongement est dérivable en
 :
:
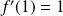 .
.
Etude en
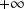 :
:
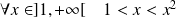 et
et
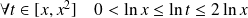 .
.
Donc :
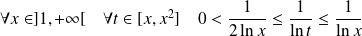 .
.
Donc :
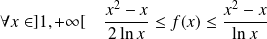 . Or :
. Or :
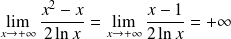 .
.
Donc :
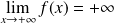 et
et
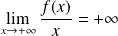 .
.
La courbe de
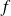 admet en
admet en
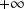 une branche parabolique de direction
une branche parabolique de direction
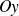 .
.