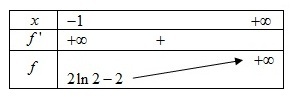
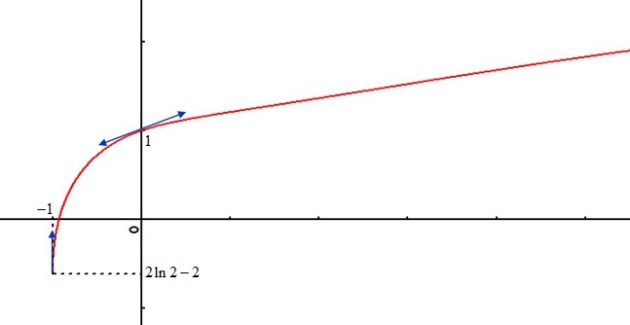
Exo 12
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Etudier la fonction
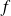définie par :
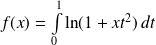et donner l'allure de sa courbe représentative.
Pour l'étude des limites, intégrez par parties et faites un changement de variable.
Soit
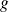la fonction définie par :
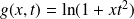. Donc :
.
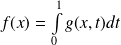Si
:
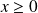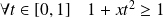. Et si
:
.
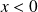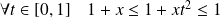Donc la fonction
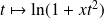est continue sur
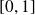si
.
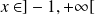Donc la fonction
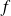est définie sur
.
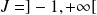Etude de la continuité :
L'intervalle
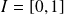est un segment et la fonction
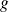est continue sur
.
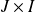Donc la fonction
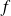est continue sur
.
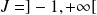Etude des variations :
La fonction
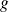admet une dérivée partielle :
.
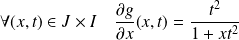L'intervalle
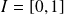est un segment et les fonctions
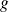et
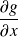sont continues sur
.
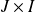Donc la fonction
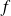est de classe
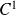sur
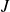et :
.
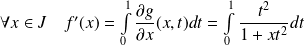Or :
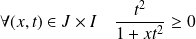. Donc :
.
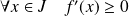Donc la fonction
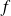est croissante sur
.
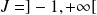Etude des limites :
On intègre par parties :
.
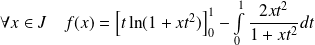Donc :
.
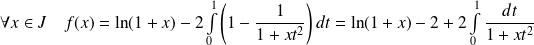Si
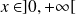, on pose :
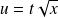, donc :
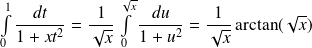.Or :
, donc :
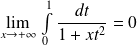. Donc :
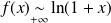.Donc :
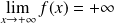et
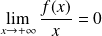.La courbe de
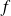admet en
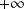une branche parabolique de direction
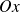.Si
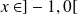, on pose :
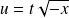, donc :
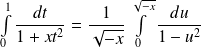.Donc :
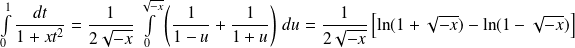.Or :
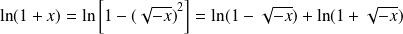.Donc :
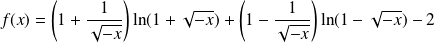.Donc :
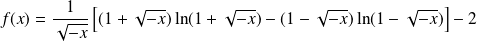.Or :
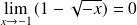, donc :
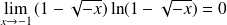. Donc :
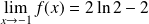.Donc la fonction
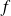est prolongeable par continuité en
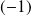en posant :
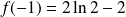.Or :
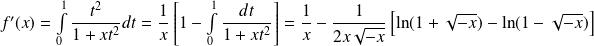.Donc :
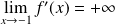. Donc le prolongement de
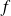n'est pas dérivable en
.
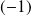D'après l'étude faite au début, la fonction
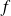est continue et dérivable en
:
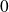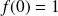et
.
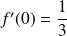