Exo 14
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
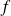 la fonction définie par :
la fonction définie par :
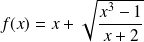 .
.
Question
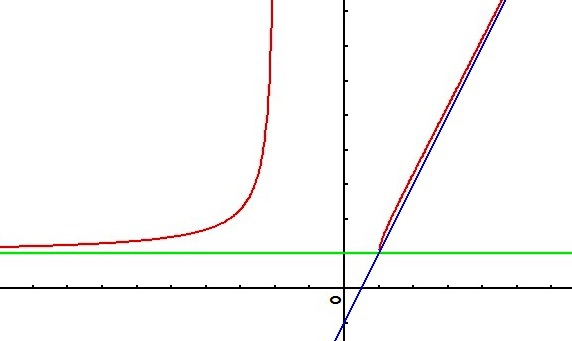
Etudier le comportement à l'infini de la fonction
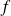 . Interpréter géométriquement.
. Interpréter géométriquement.
Posez
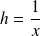 et utilisez les développements limités.
et utilisez les développements limités.
La fonction
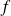 est définie si et seulement si :
est définie si et seulement si :
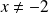 et
et
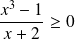 .
.
Donc l'ensemble de définition de
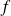 est :
est :
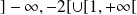 .
.
On étudie donc le comportement de f en
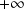 et en
et en
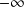 .
.
On pose :
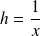 . Donc :
. Donc :
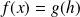 avec :
avec :
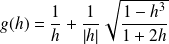 .
.
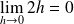 et au voisinage de
et au voisinage de
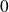 :
:
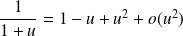 .
.
Donc :
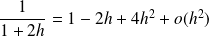 .
.
Et :
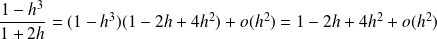 .
.
Donc :
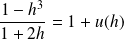 avec
avec
 , donc :
, donc :
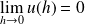 .
.
Or, au voisinage de
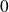 :
:
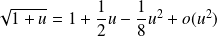 .
.
Donc :
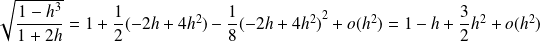 .
.
Donc :
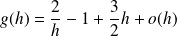 si
si
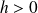 et :
et :
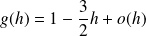 si
si
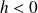 .
.
Donc, au voisinage de
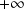 :
:
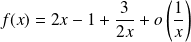 .
.
Conclusion :
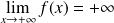 .
.
La courbe représentative de
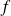 admet en
admet en
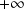 une asymptote oblique d'équation
une asymptote oblique d'équation
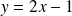 et la courbe est au dessus de l'asymptote.
et la courbe est au dessus de l'asymptote.
Et, au voisinage de
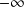 :
:
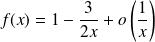 .
.
Conclusion :
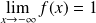 .
.
La courbe représentative de
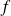 admet en
admet en
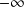 une asymptote horizontale d'équation
une asymptote horizontale d'équation
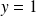 et la courbe est au dessus de l'asymptote.
et la courbe est au dessus de l'asymptote.