Applications
Méthode :
Calcul d'une limite en un point d'une fonction
Pour calculer la limite en
 d'une fonction
d'une fonction
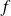 , il suffit de déterminer le
, il suffit de déterminer le
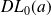 de la fonction.
de la fonction.
En effet le
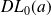 est de la forme :
est de la forme :
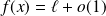 , donc :
, donc :
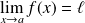 .
.
Exemple :
Exemple 1 : Calculer
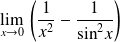 .
.
Méthode :
Calcul d'une limite à l'infini d'une fonction ou d'une limite d'une suite
Pour calculer la limite à l'infini d'une fonction
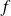 , on pose
, on pose
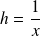 pour se ramener à la recherche d'un développement limité en
pour se ramener à la recherche d'un développement limité en
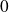 .
.
Pour une suite, la méthode est la même en posant
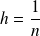 .
.
Le calcul peut conduire à des puissances négatives de
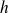 .
.
Exemple :
Exemple 2 : Calculer
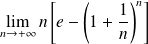 .
.
Méthode :
Recherche d'un équivalent d'une fonction ou d'une suite
On détermine le premier terme non nul du développement limité de
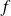 .
.
Ceci peut être utile par exemple pour étudier la convergence d'une série ou d'une intégrale.
Exemple :
Exemple 3 : Déterminer un équivalent de
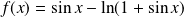 au voisinage de
au voisinage de
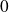 .
.
Méthode :
Etude locale d'une fonction
Si la fonction
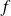 admet un
admet un
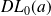 , alors
, alors
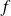 est continue en
est continue en
 .
.
Si la fonction
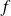 admet un
admet un
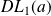 , alors
, alors
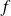 est dérivable en
est dérivable en
 .
.
La partie principale du
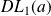 de la fonction donne l'équation de la tangente à la courbe de
de la fonction donne l'équation de la tangente à la courbe de
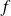 au point d'abscisse
au point d'abscisse
 .
.
Le premier terme non nul suivant permet de préciser la position de la courbe par rapport à sa tangente au voisinage du point d'abscisse
 .
.
Supposons par exemple qu'au voisinage de
 :
:
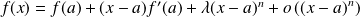 avec
avec
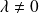 .
.
Si
 est pair et si
est pair et si
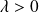 , la courbe est au dessus de sa tangente.
, la courbe est au dessus de sa tangente.Si
 est pair et si
est pair et si
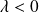 , la courbe est en dessous de sa tangente.
, la courbe est en dessous de sa tangente.Si
 est impair, la courbe traverse sa tangente au point d'abscisse
est impair, la courbe traverse sa tangente au point d'abscisse
 , donc on a un point d'inflexion.
, donc on a un point d'inflexion.
Exemple :
Exemple 4 : Etudier au voisinage de
 la fonction définie par :
la fonction définie par :
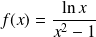 si
si
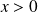 et
et
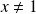 .
.
Méthode :
Etude d'une fonction à l'infini
Le principe est le même en
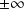 : on se ramène à une étude en
: on se ramène à une étude en
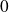 en posant
en posant
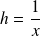 .
.
Si le développement est de la forme :
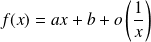 , la droite d'équation
, la droite d'équation
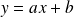 est asymptote à l'infini de la courbe de
est asymptote à l'infini de la courbe de
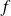 .
.
Le premier terme non nul suivant permet de préciser la position de la courbe par rapport à son asymptote.
Supposons par exemple qu'au voisinage de l'infini :
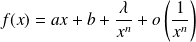 avec
avec
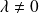 .
.
Si
 est pair et si
est pair et si
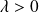 , la courbe est au dessus de son asymptote en
, la courbe est au dessus de son asymptote en
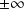 .
.Si
 est pair et si
est pair et si
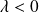 , la courbe est en dessous de son asymptote en
, la courbe est en dessous de son asymptote en
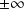 .
.Si
 est impair et si
est impair et si
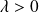 , la courbe est au dessus de son asymptote en
, la courbe est au dessus de son asymptote en
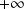 et en dessous en
et en dessous en
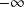 .
.Si
 est impair et si
est impair et si
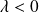 , la courbe est en dessous de son asymptote en
, la courbe est en dessous de son asymptote en
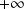 et au dessus en
et au dessus en
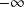 .
.
Exemple :
Exemple 5 : Etudier le comportement à l'infini de la fonction
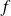 définie par
définie par
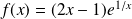 si
si
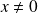 .
.





