Exo 13
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
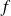la fonction définie par :
.
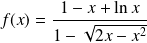Question
Montrer que la fonction
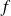est prolongeable par continuité en
, que ce prolongement est dérivable en
et préciser la position de la courbe par rapport à sa tangente au point d'abscisse
.
Déterminez un développement limité d'ordre
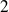de la fonction
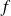en
.
On pose :
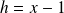. Donc :
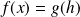avec :
.
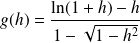Au voisinage de
:
.
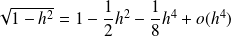Donc :
.
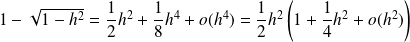Donc :
avec
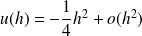, donc
.
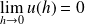Or, au voisinage de
:
.
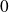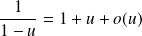Donc :
.
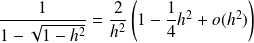Et :
.
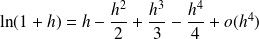Donc :
.
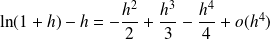Donc :
.
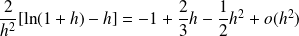Donc :
.
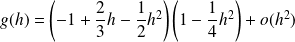Donc :
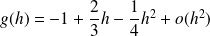au voisinage de
.
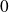Donc :
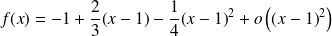au voisinage de
.
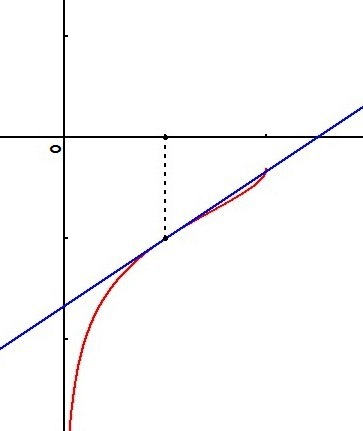
Conclusion :
La fonction
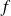est prolongeable par continuité en
en posant :
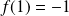.Son prolongement par continuité est dérivable en
et :
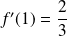.Une équation de la tangente à la courbe au point d'abscisse
est :
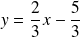.Et la courbe de
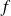est en dessous de sa tangente au voisinage de ce point.
