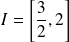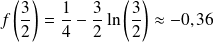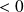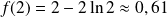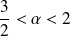Exo 11
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère la fonction
définie par :
.
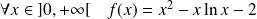Question
Démontrer que l'équation
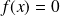admet une unique solution
.
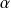Utilisez le théorème de bijection.
La fonction
est continue et dérivable sur
.
Sa dérivée est définie par :
.
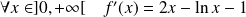La fonction
est continue et dérivable sur
.
Sa dérivée est définie par :
.
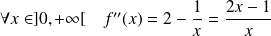Donc la fonction
est décroissante sur
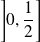et croissante sur
.
Elle admet un minimum en
et
. Donc :
.
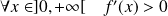Donc la fonction
est continue et strictement croissante sur
.
Elle réalise donc une bijection de
dans
.
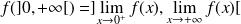Or :
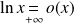. Donc :
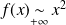, donc :
.
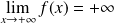Et
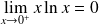, donc :
.
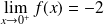Donc :
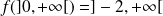, donc
.
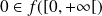Conclusion : L'équation
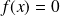admet une unique solution
.
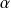Question
Question
On définit la suite
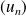par :
et
.
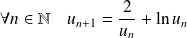Démontrer que :
.
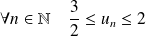Raisonnez par récurrence.
Soit
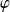la fonction définie par :
.
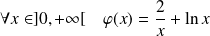La fonction
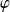est dérivable sur
et :
.
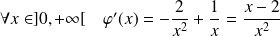Donc la fonction
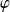est continue et décroissante sur
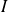. Donc :
.
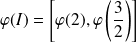Or :
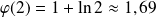et
. Donc :
.
Or :
, donc
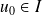et :
.
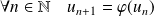Donc une récurrence évidente montre que :
.
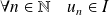Conclusion :
.
Question
Quelle est la seule limite possible de la suite
?
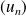Supposez que la suite converge vers
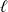et utilisez l'unicité de la limite.
Supposons que la suite
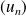converge. Soit :
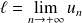. Donc :
.
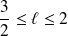La fonction
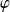est continue sur
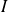. Donc :
.
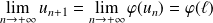Donc :
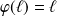, donc :
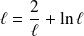, donc :
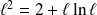, donc :
.
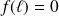Conclusion : La seule limite possible de la suite
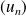est
.
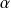Question
Démontrer que :
.
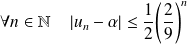Raisonnez par récurrence et utilisez l'inégalité des accroissements finis.
On raisonne par récurrence.
Initialisation :
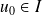et
, donc :
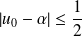, donc :
.
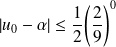Hérédité : Soit
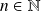tel que
.
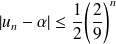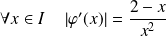. Or :
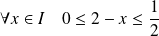et
.
Donc la fonction
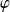est continue et dérivable sur
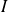, et :
.
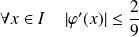Donc, d'après l'inégalité des accroissements finis :
.
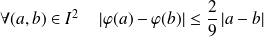Or
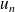et
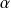appartiennent à
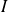, et
.
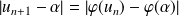Donc :
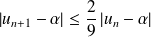. Or :
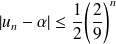. Donc :
.
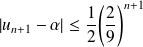Conclusion :
.
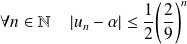Question
En déduire une valeur approchée de
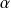à
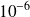près.
Déterminez
pour que
.
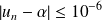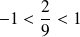, donc :
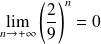. Donc :
.
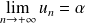Donc on peut rendre
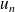aussi proche de
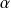que l'on veut à condition de prendre
suffisamment grand, l'erreur commise étant inférieure à
.
Donc, pour avoir une valeur approchée de
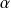à
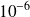près, il suffit que :
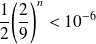, donc que :
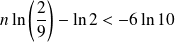, donc que :
.
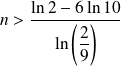Or :
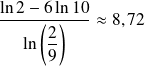. Donc il suffit de prendre
.
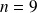Le calcul donne :
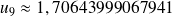. Et :
.
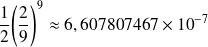Donc :
.
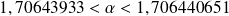Conclusion : Une valeur approchée de
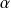à
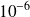près est
.
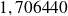