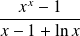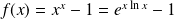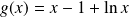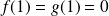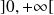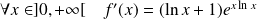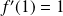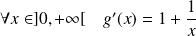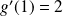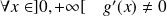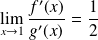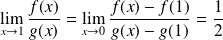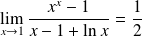Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
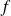et
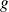deux fonctions continues sur un intervalle
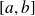et dérivables sur
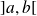(avec
).
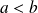Question
Démontrer qu'il existe
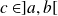tel que :
.
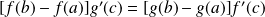Construisez une fonction
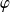à laquelle vous appliquerez le théorème de Rolle.
On construit une fonction
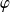à laquelle on appliquera le théorème de Rolle.
On veut que sa dérivée soit :
.
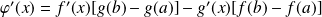Donc, on pose :
.
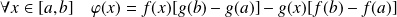La fonction
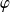est continue sur
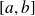et dérivable sur
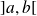comme combinaison linéaire de
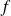et
.
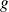Et :
.
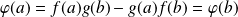Donc, d'après le théorème de Rolle, il existe
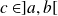tel que :
.
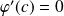Conclusion : Il existe
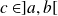tel que
.
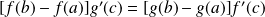Question
On suppose que :
.
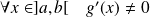Démontrer que si
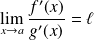(finie ou infinie), alors
.
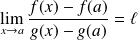Utilisez la propriété précédente entre
et
, puis faites tendre
vers
.
On peut remarquer que :
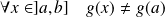car sinon, d'après le théorème de Rolle, il existerait
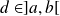tel que
.
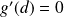D'après la première question :
.
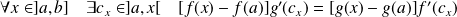Donc :
.
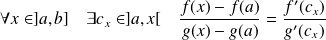Or :
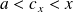. Donc :
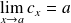. Donc :
.
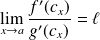Conclusion : Si
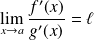, alors
.
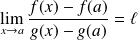Question
Question
Calculer la limite de
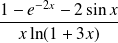quand
tend vers
.
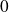Utilisez deux fois la propriété précédente.
On pose :
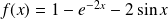et
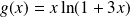. Donc :
.
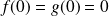La limite cherchée correspond donc à un cas d'indétermination de la forme
.
Les fonctions
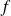et
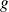sont continues et dérivables sur
.
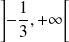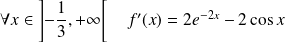, donc :
.
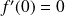Et :
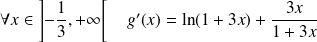, donc :
.
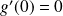Donc la limite en
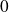de
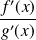correspond encore à un cas d'indétermination de la forme
.
Les fonctions
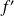et
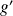sont continues et dérivables sur
.
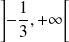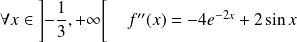, donc :
.
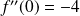Et :
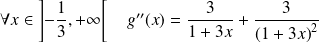, donc :
.
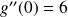Donc :
.
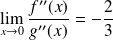Donc :
.
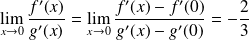Donc :
.
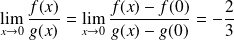Conclusion :
.
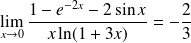