Propriétés liées à la dérivation
Attention :
Dans ce qui suit, les fonctions sont à valeurs réelles.
L'étude du signe de la dérivée d'une fonction permet de connaître ses variations.
Fondamental :
Sens de variations
Soit
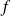une fonction dérivable sur un intervalle
.
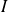Si
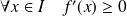, alors la fonction
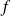est croissante sur
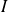.Et si
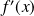ne s'annule qu'en un nombre fini de points, alors la fonction
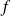est strictement croissante sur
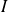.Si
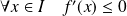, alors la fonction
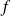est décroissante sur
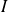.Et si
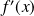ne s'annule qu'en un nombre fini de points, alors la fonction
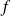est strictement décroissante sur
.
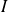Le tableau de variations d'une fonction dérivable fait donc apparaître les intervalles où la dérivée garde un signe constant, ce qui permet de déduire le sens de variations de la fonction sur ces intervalles.
Fondamental :
Théorème de Rolle
Si la fonction
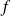est continue sur un intervalle
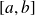, dérivable sur
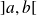et si
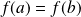, alors il existe
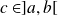tel que
.
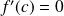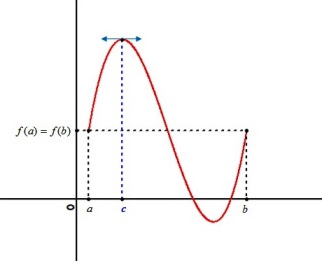
Le réel
est l'abscisse d'un point à tangente horizontale de la courbe représentative de
.
Comme le montre la figure, le réel
n'est pas toujours unique.
Le théorème donne l'existence de
, mais pas son calcul.
Fondamental :
Egalité (ou théorème) des accroissements finis
Si la fonction
est continue sur un intervalle
et dérivable sur
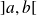, alors il existe
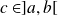tel que
.
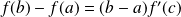Si
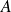et
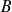sont les points de la courbe représentative de
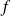d'abscisses
et
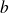, le réel
est l'abscisse d'un point où la tangente à la courbe est parallèle à la droite
.
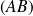Fondamental :
Inégalités des accroissements finis
Si
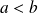, si la fonction
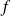est continue sur l'intervalle
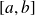, dérivable sur
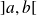et si
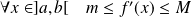, alors :
.
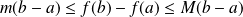Si la fonction
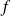est continue et dérivable sur un intervalle
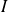, et si
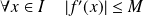, alors :
.
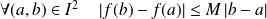La deuxième inégalité n'impose pas
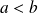. Elle est en particulier utilisée dans l'étude des suites récurrentes.
Remarque : La deuxième inégalité des accroissements finis est valable aussi pour les fonctions à valeurs complexes.
Par contre, les théorèmes précédents sont faux pour les fonctions à valeurs complexes.
Fondamental :
Prolongement de la dérivée
Si
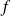est une fonction continue sur
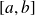, continûment dérivable[1] sur
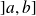et si sa dérivée
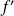admet une limite réelle en
, alors
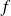est dérivable en
et
.
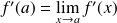Si
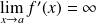, la fonction
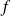n'est pas dérivable en
, et la courbe représentative de
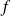admet une tangente verticale au point d'abscisse
.
