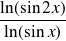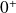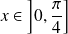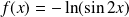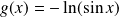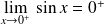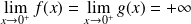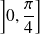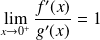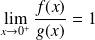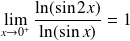Exo 9
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
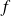et
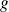deux fonctions continues sur
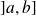et dérivables sur
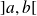avec
.
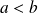On suppose que :
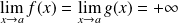, et que :
.
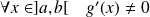Question
Démontrer que si
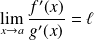(finie ou infinie), alors
.
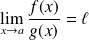Démontrez qu'il suffit d'étudier le cas où la limite
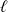est finie.
Utilisez l'exercice
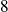entre deux réels
et
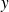, puis majorez
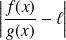en utilisant la définition de la limite de
.
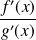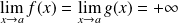. Donc au voisinage de
, les fonctions sont positives.
Quitte à réduire l'intervalle, on peut supposer que :
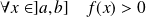et
.
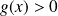D'autre part, si
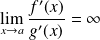, il existe un voisinage de
où
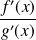, et donc
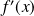, ne s'annule pas. Et
.
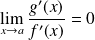Donc, quitte à échanger les deux fonctions, on peut supposer que la limite
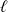est finie.
On utilise l'exercice précédent.
Pour tous
et
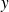vérifiant
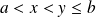, il existe un réel
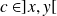tel que :
.
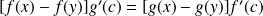Donc :
.
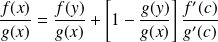Donc :
.
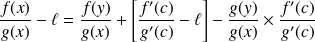Donc :
.
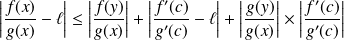Soit
.
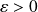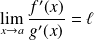, donc :
.
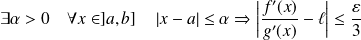On fixe
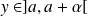. Donc :
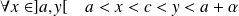. Donc :
.
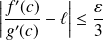Donc :
.
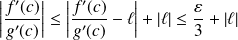Donc :
.
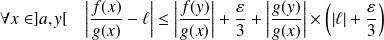Or :
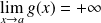, donc
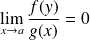et
(
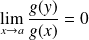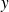est fixé).
Donc :
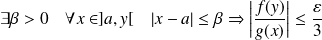et
.
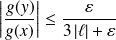Donc :
.
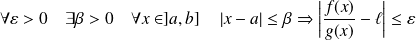Conclusion : Si
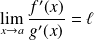(finie ou infinie), alors
.
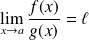