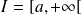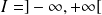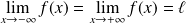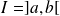Dérivation des fonctions numériques (1)

Exo 7

Commencez par chercher à résoudre l'exercice par vous-même.

Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.

Une solution détaillée vous est ensuite proposée.

On veut généraliser le théorème de Rolle.

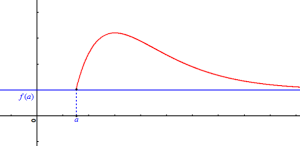
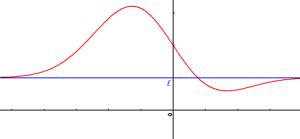
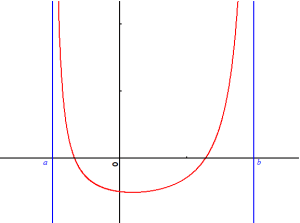
Soit 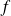une fonction dérivable sur un intervalle 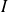et non constante (le résultat est évident si 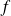est constante !).

Question

On suppose que et que : .

Démontrer qu'il existe tel que : .

Indice

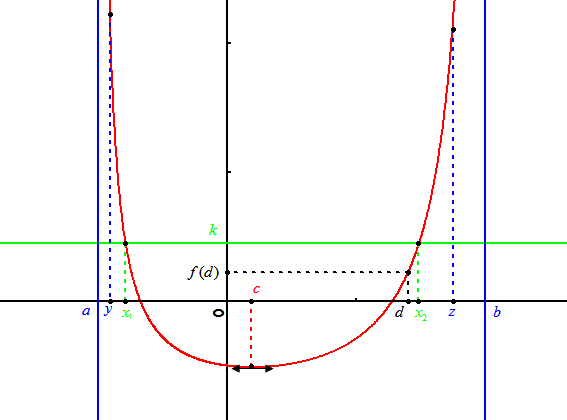
Séparez l'intervalle 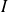en deux intervalles et construisez un réel 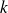tel que l'équation 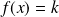ait une solution sur chacun de ces intervalles.

Utilisez ensuite le théorème de Rolle.

Solution

La fonction 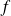n'est pas constante. Donc il existe 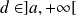tel que : .

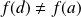On suppose par exemple : 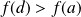et on pose : .

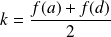Sur l'intervalle 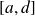, la fonction 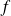est continue. Elle prend les valeurs 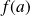et 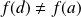, donc elle prend toute valeur intermédiaire.

Or : 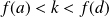. Donc il existe 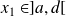tel que : .

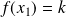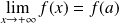, donc : .

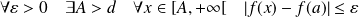Donc pour : .

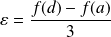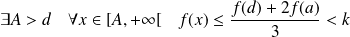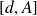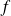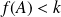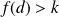Sur l'intervalle , la fonction est continue. Elle prend les valeurs et , donc elle prend toute valeur intermédiaire. Donc il existe 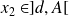tel que : .

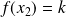La fonction 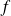est continue sur 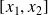, dérivable sur 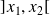et .

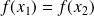Donc, d'après le théorème de Rolle, il existe 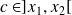tel que : .

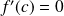Conclusion : Il existe 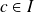tel que : .

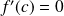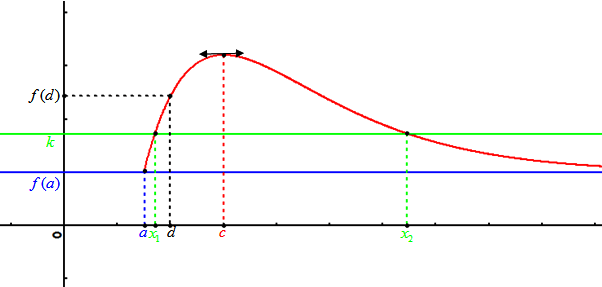
Question

On suppose que et que (limite finie).

Démontrer qu'il existe tel que : .

Indice

Utilisez la même méthode.

Solution

La fonction 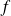n'est pas constante. Donc il existe 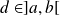tel que : .

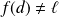On suppose par exemple : 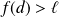et on pose : .

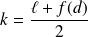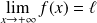, donc : .

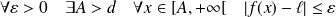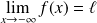, donc : .

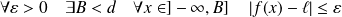Pour 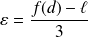: 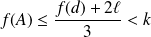et .

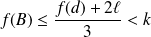Sur l'intervalle 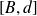, la fonction 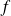est continue. Elle prend les valeurs 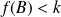et 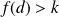, donc elle prend toute valeur intermédiaire. Donc il existe 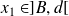tel que : .

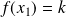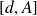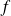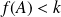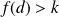Sur l'intervalle , la fonction est continue. Elle prend les valeurs et , donc elle prend toute valeur intermédiaire. Donc il existe 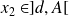tel que : .

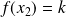La fonction 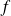est continue sur 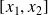, dérivable sur 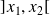et .

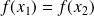Donc, d'après le théorème de Rolle, il existe 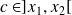tel que : .

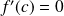Conclusion : Il existe 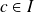tel que : .

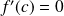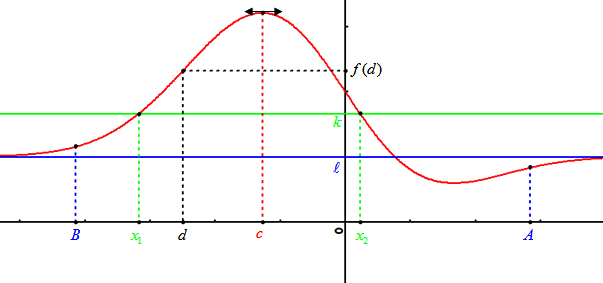
Question

On suppose que et que : .

Démontrer qu'il existe tel que : .

Indice

Utilisez la même méthode.

Solution

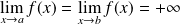. Donc il existe 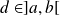tel que 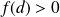. Soit : .

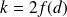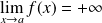, donc : .

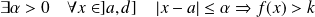Sur l'intervalle 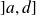, la fonction 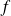est continue. Elle prend la valeur 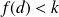et une valeur 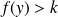si 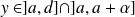, donc elle prend toute valeur intermédiaire. Donc il existe 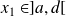tel que : .

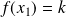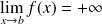, donc : .

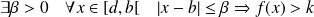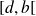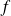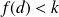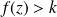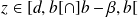Sur l'intervalle , la fonction est continue. Elle prend la valeur et une valeur si , donc elle prend toute valeur intermédiaire. Donc il existe 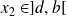tel que : .

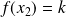La fonction 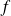est continue sur 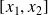, dérivable sur 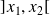et .

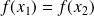Donc, d'après le théorème de Rolle, il existe 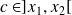tel que : .

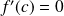Conclusion : Il existe tel que : .

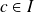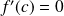PrécédentPrécédentSuivantSuivant
AccueilAccueilImprimerImprimer Paternité - Pas d'Utilisation Commerciale - Partage des Conditions Initiales à l'IdentiqueRéalisé avec Scenari (nouvelle fenêtre)