Exo 7
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère l'espace euclidien
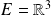 orienté par sa base canonique
orienté par sa base canonique
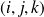 .
.
On dira qu'une application
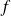 de
de
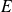 dans
dans
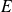 conserve le produit vectoriel si elle vérifie la propriété :
conserve le produit vectoriel si elle vérifie la propriété :
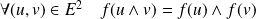 .
.
Question
Démontrer que toute rotation vectorielle conserve le produit vectoriel.
Utilisez le produit mixte et la bijectivité de
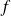 .
.
Remarquez que :
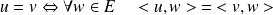 .
.
Remarque :
Dans ce qui suit, le produit scalaire de deux vecteurs
 et
et
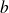 est noté
est noté
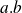 au lieu de
au lieu de
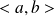 .
.
Soit
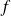 une rotation vectorielle, donc bijective. Donc :
une rotation vectorielle, donc bijective. Donc :
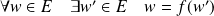 .
.
Donc :
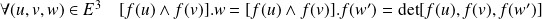 .
.
Donc :
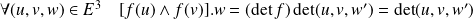 car
car
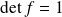 .
.
Donc :
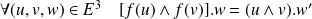 . Or
. Or
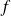 conserve le produit scalaire.
conserve le produit scalaire.
Donc :
 .
.
Conclusion :
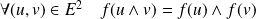 .
.
Question
Démontrer que si
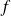 est une application non nulle de
est une application non nulle de
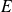 dans
dans
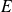 qui conserve le produit vectoriel, alors :
qui conserve le produit vectoriel, alors :
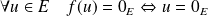 .
.
Raisonnez par l'absurde en supposant qu'il existe
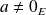 tel que
tel que
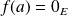 .
.
Utilisez alors
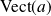 et son supplémentaire orthogonal.
et son supplémentaire orthogonal.
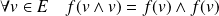 . Or :
. Or :
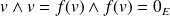 . Donc :
. Donc :
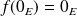 .
.
Réciproquement, montrons qu'il n'existe pas
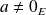 tel que
tel que
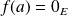 .
.
On raisonne par l'absurde : on suppose qu'il existe
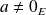 tel que
tel que
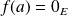 . Soit
. Soit
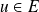 .
.
Si
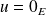 , alors, d'après ce qui précède :
, alors, d'après ce qui précède :
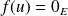 .
.
Supposons
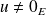 . Soit
. Soit
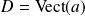 et
et
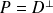 . Alors :
. Alors :
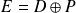 .
.
Donc il existe un réel
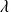 et un vecteur
et un vecteur
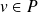 tels que :
tels que :
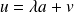 .
.
Supposons que
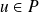 . Donc
. Donc
 est orthogonal à
est orthogonal à
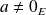 . Donc il existe un vecteur
. Donc il existe un vecteur
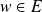 tel que
tel que
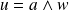 . Donc :
. Donc :
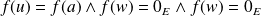 .
.
Supposons que
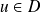 . Soit un vecteur
. Soit un vecteur
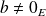 appartenant à
appartenant à
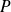 .
.Donc
 est orthogonal à
est orthogonal à
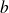 . Donc il existe
. Donc il existe
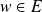 tel que
tel que
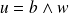 .
.Or
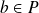 . Donc, d'après ce qui précède :
. Donc, d'après ce qui précède :
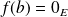 .
.Donc :
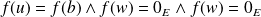 .
.
Supposons que
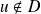 . Donc
. Donc
 et
et
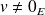 sont indépendants, donc
sont indépendants, donc
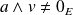 .
.Or
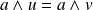 . Donc
. Donc
 est orthogonal à
est orthogonal à
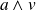 .
.Donc il existe
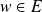 tel que :
tel que :
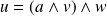 . Donc
. Donc
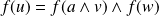 .
.Or
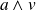 est orthogonal à
est orthogonal à
 , donc
, donc
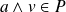 , donc
, donc
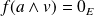 .
.Donc :
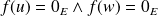 .
.
Donc :
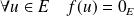 . Or par hypothèse,
. Or par hypothèse,
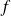 n'est pas l'application nulle.
n'est pas l'application nulle.
Donc il n'existe pas
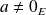 tel que
tel que
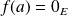 . Donc :
. Donc :
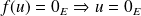 .
.
Conclusion :
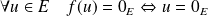 .
.
Question
Démontrer que tout endomorphisme non nul de
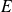 qui conserve le produit vectoriel est une rotation.
qui conserve le produit vectoriel est une rotation.
Démontrez que
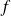 transforme une base orthonormale directe
transforme une base orthonormale directe
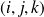 en une base orthonormale directe.
en une base orthonormale directe.
Soit
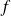 un endomorphisme non nul qui vérifie :
un endomorphisme non nul qui vérifie :
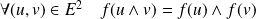 .
.
Montrons que
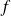 transforme la base orthonormale directe
transforme la base orthonormale directe
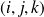 en une base orthonormale directe.
en une base orthonormale directe.
Montrons que les images de deux vecteurs
 et
et
 orthogonaux sont orthogonales.
orthogonaux sont orthogonales.Si
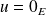 , alors
, alors
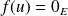 , donc
, donc
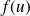 et
et
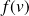 sont orthogonaux.
sont orthogonaux.Si
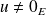 , alors il existe un vecteur
, alors il existe un vecteur
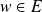 non nul tel que :
non nul tel que :
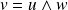 .
.Donc :
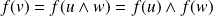 . Donc
. Donc
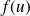 et
et
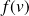 sont orthogonaux.
sont orthogonaux.Donc les vecteurs
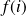 ,
,
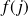 et
et
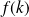 sont deux à deux orthogonaux.
sont deux à deux orthogonaux.
Montrons que les vecteurs
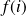 ,
,
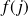 et
et
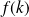 sont unitaires.
sont unitaires.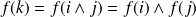 . Et les vecteurs
. Et les vecteurs
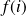 et
et
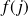 sont orthogonaux.
sont orthogonaux.Donc :
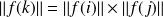 .
. De même :
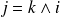 . Donc :
. Donc :
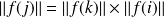 .
.Donc :
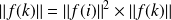 . Or
. Or
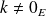 , donc
, donc
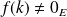 , donc
, donc
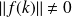 .
.Donc :
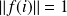 . Un raisonnement analogue donne :
. Un raisonnement analogue donne :
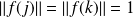 .
.Donc les vecteurs
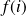 ,
,
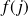 et
et
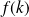 sont unitaires.
sont unitaires.
Montrons que les vecteurs
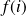 ,
,
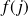 et
et
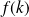 forment une base orthonormale directe.
forment une base orthonormale directe.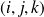 est une base orthonormale directe, donc :
est une base orthonormale directe, donc :
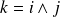 .
.Donc par conservation du produit vectoriel :
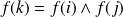 .
.Donc les vecteurs
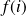 ,
,
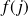 et
et
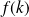 forment une base orthonormale directe.
forment une base orthonormale directe.
Donc
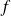 est un endomorphisme qui transforme une base orthonormale directe en une base orthonormale directe. Donc
est un endomorphisme qui transforme une base orthonormale directe en une base orthonormale directe. Donc
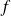 est une rotation vectorielle.
est une rotation vectorielle.
Conclusion : Tout endomorphisme non nul de
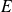 qui conserve le produit vectoriel est une rotation.
qui conserve le produit vectoriel est une rotation.





