Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère l'espace euclidien
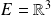rapporté à sa base canonique.
Question
Déterminer la nature et les éléments caractéristiques de l'endomorphisme
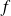de matrice :
.
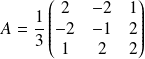Démontrez que
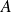est une matrice orthogonale et remarquez qu'elle est symétrique.
.
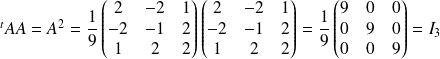Et :
.
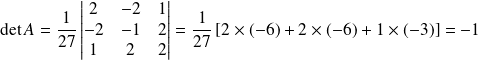Donc
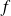est un endomorphisme orthogonal indirect et
.
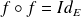Donc
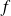est une réflexion par rapport au plan :
.
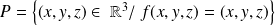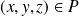si et seulement si :
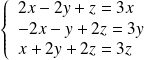, donc si :
.
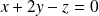Conclusion :
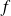est la réflexion par rapport au plan d'équation
.
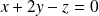Question
Déterminer la nature et les éléments caractéristiques de l'endomorphisme
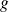de matrice :
.
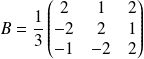Démontrez que
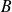est une matrice orthogonale et calculez son déterminant.
.
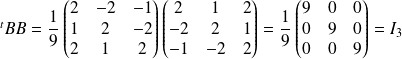Et :
.
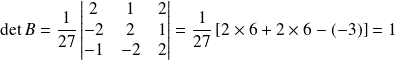Donc
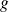est un endomorphisme orthogonal direct et
.
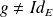Donc
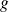est une rotation vectorielle. Soit
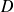son axe et
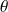son angle.
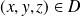si et seulement si :
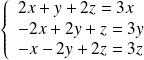, donc si :
.
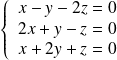Donc l'axe
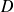de
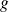est la droite d'équation :
.
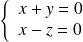Le vecteur
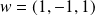oriente
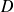et le plan
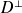d'équation :
.
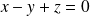Le vecteur
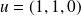appartient à
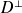et a pour image :
.
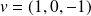La trace de
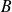est
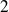. Donc :
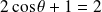, donc
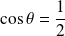. Donc :
.
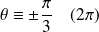Or
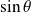est du signe de
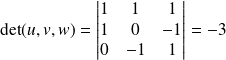, donc :
.
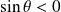Conclusion :
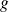est la rotation vectorielle d'axe
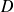orienté par
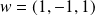et d'angle
.
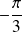Question
Déterminer la nature et les éléments caractéristiques de l'endomorphisme
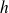de matrice :
.
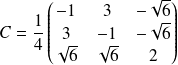Démontrez que
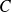est une matrice orthogonale et calculez son déterminant.
.
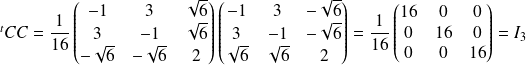Et :
.
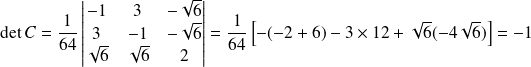Donc
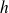est un endomorphisme orthogonal indirect dont la matrice n'est pas symétrique et
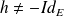. Donc
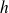est composée d'une rotation
et d'une réflexion
.
L'axe de la rotation est l'ensemble des vecteurs
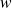tels que
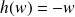, donc tels que :
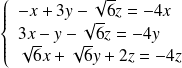, donc tels que :
.
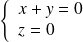Donc l'axe
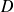de la rotation est la droite vectorielle orientée par
.
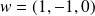Donc le plan de la réflexion
est
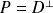d'équation
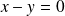orienté par
.
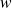Donc pour tout vecteur
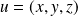, on a :
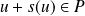et
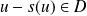, donc il existe un réel
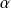tel que
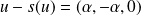, donc
.
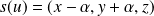Or
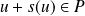, donc :
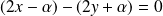, donc :
.
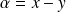Donc :
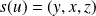. Donc la matrice de
est :
.
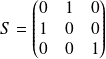On a :
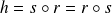, donc la rotation est
.
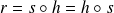Donc la matrice de
est :
.
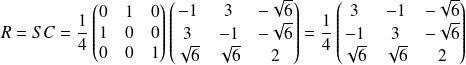Son angle
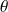vérifie
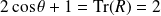, donc
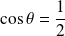, donc
.
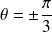Le vecteur
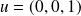appartient à
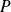et a pour image
.
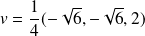Or
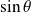est du signe de
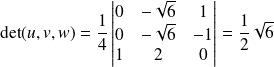, donc :
.
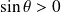Conclusion :
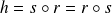où
est la réflexion par rapport au plan d'équation
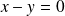, et
la rotation d'axe orienté par
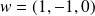et d'angle
.
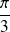