Exo 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
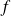l'endomorphisme de
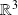de matrice
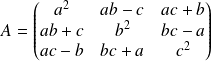dans la base canonique
.
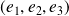Question
Déterminer les réels
,
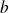et
pour que
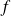soit un endomorphisme orthogonal.
Un endomorphisme est orthogonal si et seulement si il transforme une base orthonormale en base orthonormale.
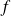est un endomorphisme orthogonal si et seulement si l'image de la base canonique (orthonormale) est une base orthonormale, donc si
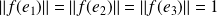et
.
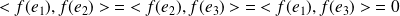Or :
.
.
.
.
.
.
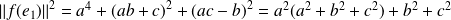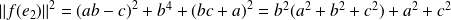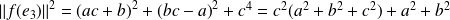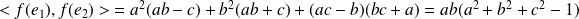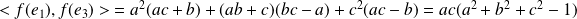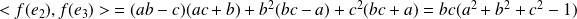Si
,
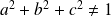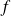est orthogonal si et seulement si
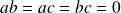et
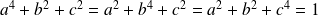. On obtient
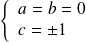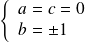ou
ou
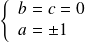ce qui est contradictoire avec
.
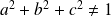Par contre, si
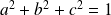, la famille
,
,
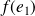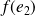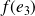est orthonormale.
Conclusion :
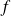est un endomorphisme orthogonal si et seulement si
.
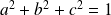Question
Préciser sa nature et ses caractéristiques.
Calculez le déterminant de
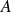pour trouver la nature de
.
.
.
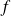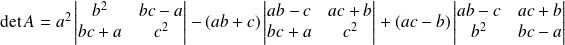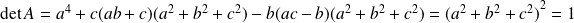Donc
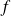est une rotation vectorielle. Soit
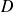son axe et
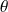son angle.
On peut remarquer que :
.
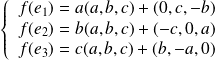Donc :
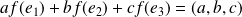puisque
.
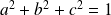Donc si
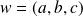, alors
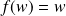, donc
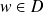. Donc :
.
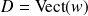Et :
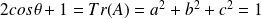. Donc :
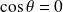. Donc :
.
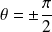Le vecteur
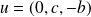est orthogonal à
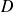et a pour image
.
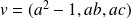Donc
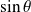est du signe de
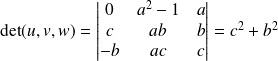. Donc
.
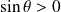Conclusion :
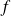est la rotation vectorielle d'axe
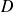orienté par
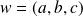et d'angle
.
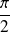