Exo 10
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
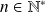 et l'application
et l'application
 qui à tout polynôme
qui à tout polynôme
 associe le reste de la division euclidienne de
associe le reste de la division euclidienne de
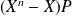 par
par
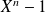 .
.
Question
Montrer que
 est un endomorphisme de
est un endomorphisme de
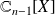 .
.
Explicitez la division euclidienne et montrez que
 est linéaire.
est linéaire.
Pour tout
 , il existe un unique couple de polynômes
, il existe un unique couple de polynômes
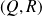 tel que :
tel que :
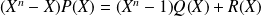 avec
avec
 . Et
. Et
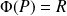 .
.
Donc
 est une application de
est une application de
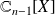 dans
dans
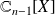 .
.
Soient
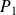 et
et
 deux polynômes de
deux polynômes de
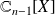 , et
, et
 un complexe.
un complexe.
 avec
avec
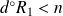 . Et
. Et
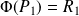 .
.
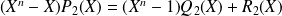 avec
avec
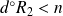 . Et
. Et
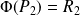 .
.
 .
.
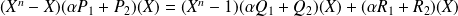 .
.
Or :
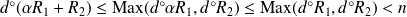 .
.
Donc
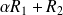 est le reste de la division euclidienne de
est le reste de la division euclidienne de
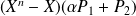 par
par
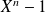 .
.
Donc
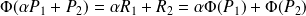 .
.
Conclusion :
 est un endomorphisme de
est un endomorphisme de
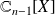 .
.
Question
Déterminer le noyau et l'image de l'endomorphisme
 .
.
Commencez par déterminer le noyau de
 en utilisant les racines
en utilisant les racines
 èmes de l'unité.
èmes de l'unité.
Puis utilisez le théorème du rang pour trouver l'image de
 .
.
Un polynôme
 appartient à
appartient à
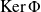 si et seulement si
si et seulement si
 , donc si
, donc si
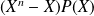 est divisible par
est divisible par
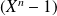 , donc si il existe un polynôme
, donc si il existe un polynôme
 tel que
tel que
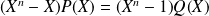 .
.
Or
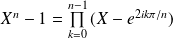 . Donc
. Donc
 appartient à
appartient à
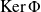 si et seulement si :
si et seulement si :
 .
.
Donc
 appartient à
appartient à
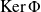 si et seulement si
si et seulement si
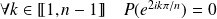 .
.
Or
 . Donc
. Donc
 est de la forme
est de la forme
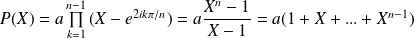 .
.
La réciproque est évidente car si
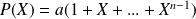 , alors
, alors
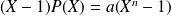 , donc est divisible par
, donc est divisible par
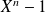 .
.
Or
 . Donc
. Donc
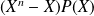 est divisible par
est divisible par
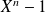 . Donc
. Donc
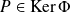 .
.
Conclusion :
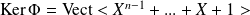 .
.
Donc
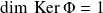 . Donc d'après le théorème du rang :
. Donc d'après le théorème du rang :
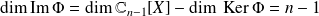 .
.
De plus
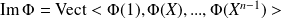 .
.
Or si
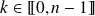 :
:
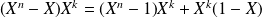 et
et
 si
si
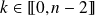 .
.
Donc
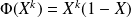 si
si
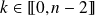 .
.
Et :
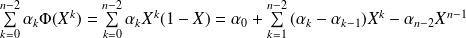 .
.
Donc
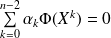 si et seulement si
si et seulement si
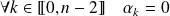 .
.
Donc la famille
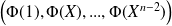 est libre. Elle comprend
est libre. Elle comprend
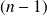 vecteurs.
vecteurs.
Donc c'est une base de
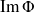 car
car
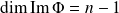 . Donc
. Donc
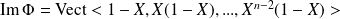 .
.
Conclusion :
 .
.





