Exo 9
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
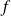 un endomorphisme d'un espace vectoriel
un endomorphisme d'un espace vectoriel
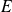 .
.
Question
Démontrer que :
 .
.
Puis démontrer que :
 .
.
Démontrez l'équivalence par double implication.
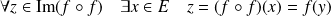 en posant
en posant
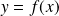 . Donc
. Donc
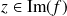 .
.
Conclusion :
 .
.
Montrons l'équivalence en deux étapes :
Supposons que :
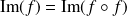 .
. , donc
, donc
 . Donc
. Donc
 .
.Donc :
 , donc
, donc
 appartient à
appartient à
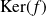 .
.Donc :
 , donc
, donc
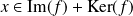 .
.Donc :
 . Or
. Or
 .
. Donc :
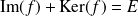 .
.Réciproquement, supposons que :
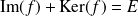 .
.Soit
 . Donc il existe
. Donc il existe
 tel que
tel que
 .
.Or
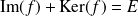 , donc
, donc
 avec
avec
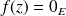 .
.Donc
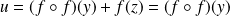 , donc
, donc
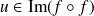 .
.Donc
 . Or
. Or
 .
. Donc
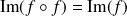 .
.
Conclusion :
 .
.
Question
Démontrer que :
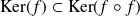 .
.
Puis démontrer que :
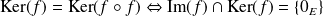 .
.
Démontrez l'équivalence par double implication.
 , donc
, donc
 , donc
, donc
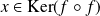 .
.
Conclusion :
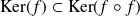 .
.
Montrons l'équivalence en deux étapes :
Supposons que :
 .
.Soit
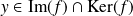 . Donc
. Donc
 et il existe
et il existe
 tel que
tel que
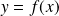 .
.Donc
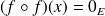 , donc
, donc
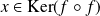 , donc
, donc
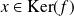 , donc
, donc
 .
.Donc :
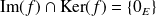 .
.
Réciproquement, supposons que :
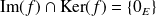 .
.Soit
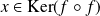 . Donc :
. Donc :
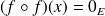 , donc
, donc
 . Or
. Or
 .
.Donc
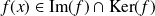 , donc
, donc
 , donc
, donc
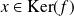 .
.Donc
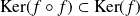 . Or
. Or
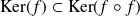 .
. Donc
 .
.
Conclusion :
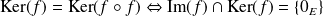 .
.





