Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
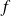l'application définie par :
.
Question
Montrer que
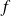est un endomorphisme de
.
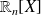Commencez par démontrer que
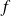est linéaire.
Puis démontrez que
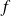est une application de
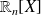dans
.
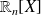Soient
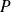et
deux polynômes de
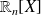et
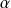un réel.
.
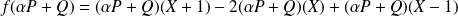Donc :
.
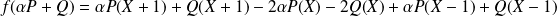Donc :
.
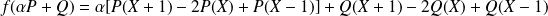Donc :
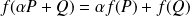. Donc l'application
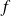est linéaire.
De plus :
.
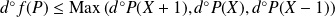Or :
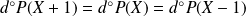. Donc si
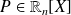, alors :
.
Donc si
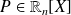, alors :
.
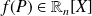Conclusion : L'application
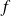est un endomorphisme de
.
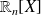Question
Déterminer le noyau et l'image de l'endomorphisme
.
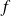Commencez par déterminer l'image de
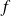en cherchant l'image de la base canonique de
.
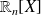Puis, à l'aide du théorème du rang, déterminez le noyau de
.
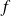Une base de
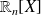est
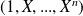. Donc :
.
Or
et
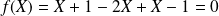. Donc :
.
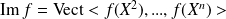Et :
.
On développe avec la formule du binôme et l'on constate que les coefficients de
et de
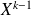s'annulent.
Donc :
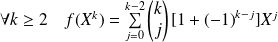et donc :
.
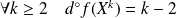Ces
polynômes étant échelonnés, ils forment une famille libre de
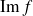, et donc une base de
.
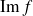Donc :
.
De plus,
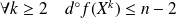. Donc :
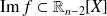. Or :
.
Conclusion :
.
D'après le théorème du rang :
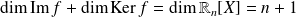. Donc
.
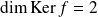Donc une base de
est formée de deux vecteurs indépendants. Or on a vu que
.
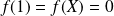Donc les polynômes
et
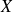appartiennent à
. Donc
.
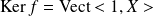Conclusion :
.
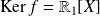Remarque :
On aurait pu déterminer directement
.
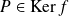si et seulement si
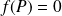, donc si
.
Donc si
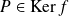, alors :
. Soit
cette constante.
Donc la suite
est arithmétique de raison
. Donc
.
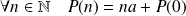Donc il existe
et
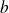réels tels que :
.
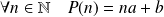Donc le polynôme
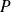coïncide sur une infinité de valeurs avec le polynôme
.
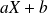Donc si
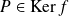, il existe
et
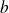réels tels que
.
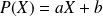Réciproquement, si
:
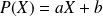, donc
.
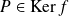Donc :
.
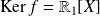