Noyau et Image
Définition :
Soit
une application linéaire d'un espace vectoriel
dans un espace vectoriel
.
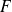Le noyau de l'application linéaire
est :
.
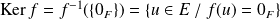C'est un sous-espace vectoriel de
.
Propriété :
L'application linéaire
est injective si et seulement si :
.
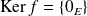Définition :
Soit
une application linéaire d'un espace vectoriel
dans un espace vectoriel
.
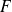L'image de l'application linéaire
est :
.
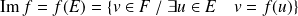C'est un sous-espace vectoriel de
.
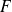Propriété :
L'application linéaire
est surjective si et seulement si :
.
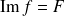Fondamental :
Soit
une application linéaire d'un espace vectoriel
de dimension finie dans un espace vectoriel
.
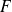Théorème du rang :
.
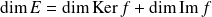Si
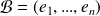est une base de
, alors
.
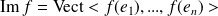Le rang d'une application linéaire est la dimension de son image.
Fondamental :
Bijectivité en dimension finie
Soit
une application linéaire d'un espace vectoriel
de dimension finie dans un espace vectoriel
.
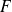Si l'application linéaire
est bijective, alors
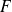est de dimension finie et
.
Et, si
est une application linéaire d'un espace vectoriel
dans un espace vectoriel
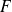tels que
, il y a équivalence entre : -
est injective.
-
est surjective.
-
est bijective.
Une application linéaire
de
dans
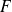est bijective si et seulement si elle transforme une base de
en une base de
.
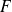