Exo 7
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
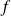l'application linéaire de
dans
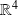dont la matrice est :
dans les bases canoniques.
Question
Déterminer son noyau et son image.
Pour le noyau, résolvez l'équation matricielle
.
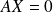Pour l'image, déterminez une famille génératrice, puis utilisez le théorème du rang.
Si un vecteur
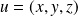a pour matrice
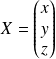, son image a pour matrice
.
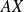Donc
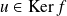si et seulement si
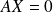, donc si :
.
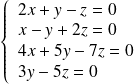Le système équivaut à :
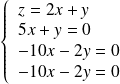, donc à
.
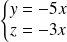Donc
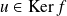si et seulement si
.
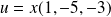Conclusion :
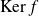est la droite vectorielle de
de base
.
Donc
et d'après le théorème du rang :
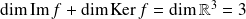. Donc :
.
Or :
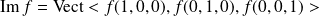. Donc :
.
Cette famille génératrice est liée car
. Pour trouver une base de
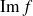, il suffit d'en extraire une famille libre de deux vecteurs, donc de choisir deux vecteurs non colinéaires, par exemple les deux premiers.
Conclusion :
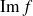est le plan vectoriel de
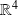de base
et
.
Donc un vecteur
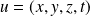de
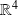appartient à
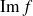si et seulement si il existe des réels
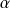et
tels que
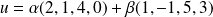, ce qui équivaut au système
.
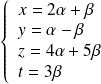Ce système admet des solutions
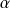et
si et seulement si :
.
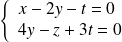Conclusion :
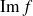est l'ensemble des vecteurs
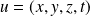de
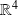tels que
.
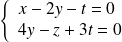