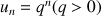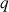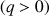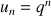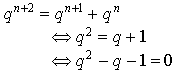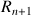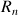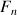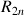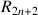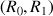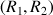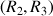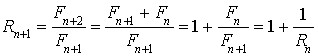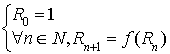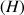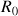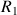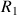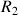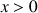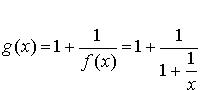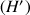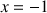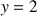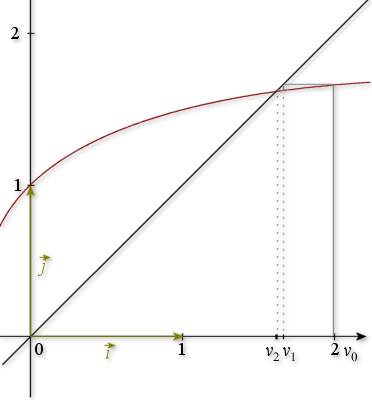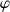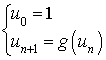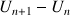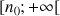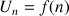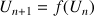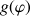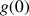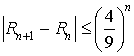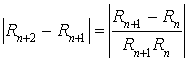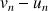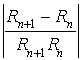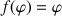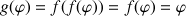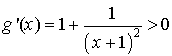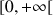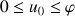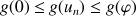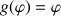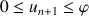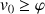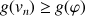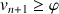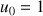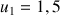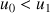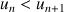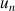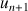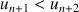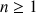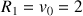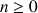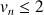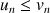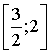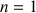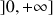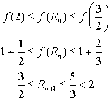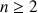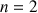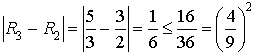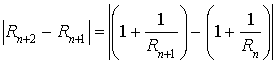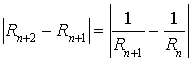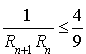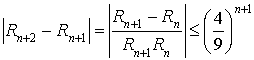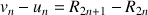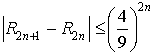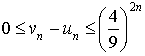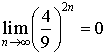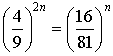Suites de Fibonacci et nombre d'or
Introduction
Durée : 90 minutes
Niveau : très difficile
On appelle suite de Fibonacci toute suite ![]() vérifiant pour tout entier naturel
vérifiant pour tout entier naturel
 :
:
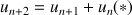
1) Montrer qu'il existe une seule suite géométrique à termes positifs vérifiant la relation (*), et de premier terme 1. Montrer que cette suite a pour raison le nombre 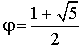 , solution positive de l'équation
, solution positive de l'équation
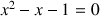 . Rappelons que ce nombre s'appelle le nombre d'or.
. Rappelons que ce nombre s'appelle le nombre d'or.
2) On considère la suite de Fibonacci
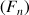 telle que
telle que
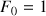 et
et
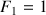 .
.
On pose pour tout entier naturel
 :
: 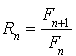 .
.
a. Calculer les termes des suites
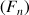 et
et
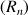 , pour
, pour
 allant de 1 à 6.
allant de 1 à 6.
b. Montrer que ![]() ,
, ![]() ,
,
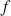 étant la fonction définie pour
étant la fonction définie pour
 strictement positif par
strictement positif par ![]() .
.
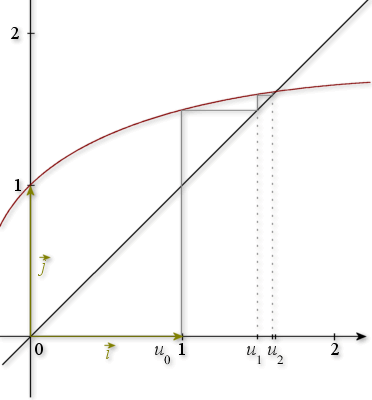
Représenter la fonction
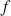 , et sur un même graphique la droite d'équation
, et sur un même graphique la droite d'équation
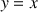 ; utiliser ce graphique pour déterminer graphiquement les premiers termes de la suite
; utiliser ce graphique pour déterminer graphiquement les premiers termes de la suite
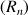 (ou utiliser l'outil mis à votre disposition).
(ou utiliser l'outil mis à votre disposition).
c. On note, ![]() :
: ![]() et
et ![]() (la suite est constituée par les termes d'indice pair de la suite
(la suite est constituée par les termes d'indice pair de la suite
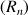 et
et
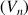 des termes d'indice impair de la suite
des termes d'indice impair de la suite
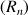 ).
).
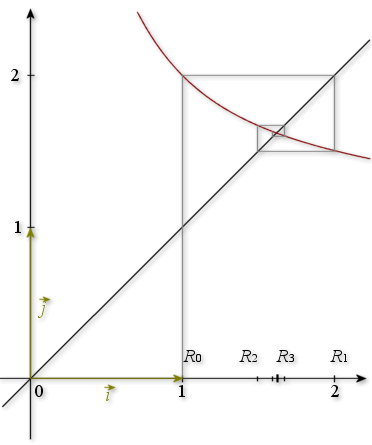
Montrer que ![]() ,
, ![]() ,
,
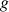 étant la fonction définie pour
étant la fonction définie pour
 strictement positif par
strictement positif par ![]() .
.
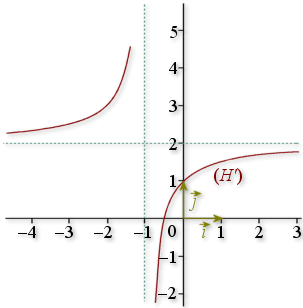
Représenter la fonction
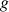 , et sur un même graphique la droite d'équation
, et sur un même graphique la droite d'équation
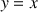 ; utiliser ce graphique pour déterminer graphiquement les premiers termes des suites
; utiliser ce graphique pour déterminer graphiquement les premiers termes des suites
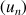 et
et
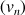 (ou utiliser l'outil mis à votre disposition).
(ou utiliser l'outil mis à votre disposition).
d. Etablir une conjecture sur :
la convergence de la suite
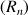 ,
,le comportement de la suite
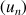 ,
,le comportement de la suite
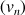 ,
,la limite des suites
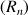 ,
,
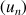 ,
,
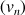 .
.
3) a. Montrer que : ![]() ,
, ![]() .
.
b. Montrer que la suite
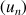 est croissante puis que la suite
est croissante puis que la suite
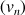 est décroissante.
est décroissante.
c. Montrer que ![]() .
.
En déduire par récurrence : 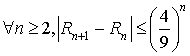 .
.
d. Montrer que les suites
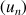 et
et
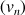 sont adjacentes, et donner leur limite commune.
sont adjacentes, et donner leur limite commune.