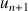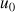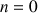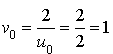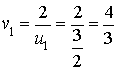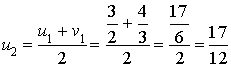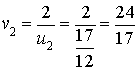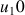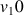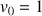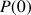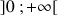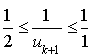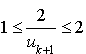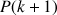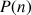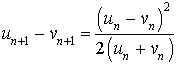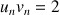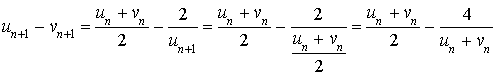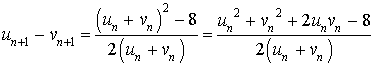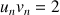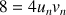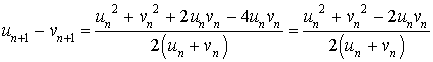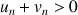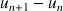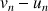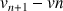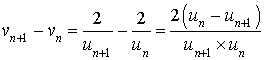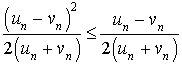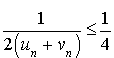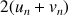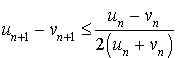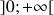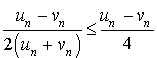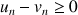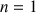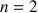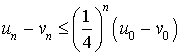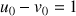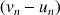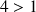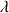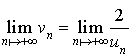Deux suites adjacentes de nombres rationnels
Introduction
Durée : 90 minutes
Niveau : très difficile
On considère les suites
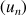 et
et
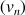 définies par :
définies par :
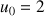 et pour tout
et pour tout
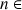 N,
N, 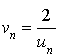 et
et 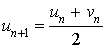 .
.
1) a. Calculer
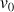 ,
,
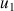 ,
,
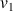 ,
,
 ,
,
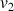 . Donner les résultats sous forme de fraction irréductible.
. Donner les résultats sous forme de fraction irréductible.
b. En utilisant un tableur (ou une calculatrice), donner un tableau de valeurs décimales approchées de
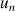 et
et
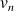 pour
pour
 variant de 1 à 10.
variant de 1 à 10.
2) Démontrer que les suites
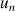 et
et
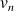 sont majorées par 2 et minorées par 1.
sont majorées par 2 et minorées par 1.
6) Montrer que pour tout
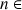 N :
N : ![]() et en déduire que :
et en déduire que : ![]() .
.
7) Montrer que pour tout
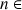 N :
N : ![]() .
.
En déduire que pour tout
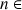 N :
N : ![]() .
.
8) Montrer que les suites
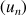 et
et
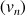 sont adjacentes et donner leur limite commune.
sont adjacentes et donner leur limite commune.
Une suite convergente de nombres rationnels a-t-elle nécessairement pour limite un nombre rationnel ?