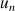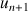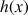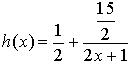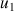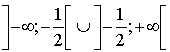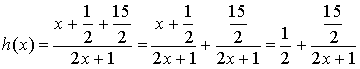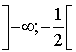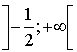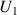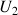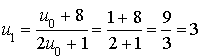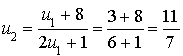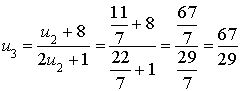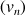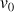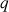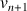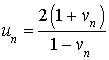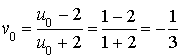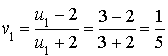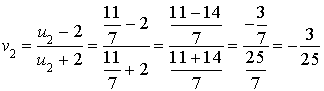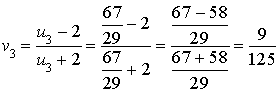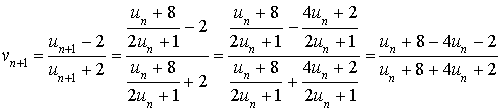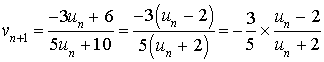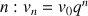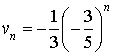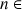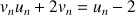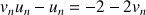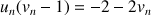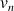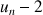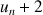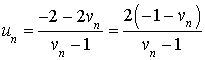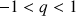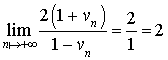Une suite définie par récurrence
Introduction
Durée : 45 minutes
Niveau : moyen
Une suite définie par récurrence
On définit la suite
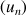par :
son terme initial
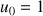;la relation de récurrence :
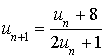pour tout entier naturel
.
Soit la fonction
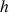définie pour 
par 
et
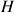sa courbe représentative.
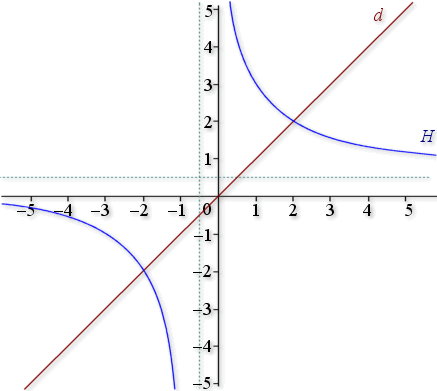
1) a. Tracer
et la droite
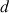d'équation
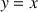dans un repère orthonormal 
.
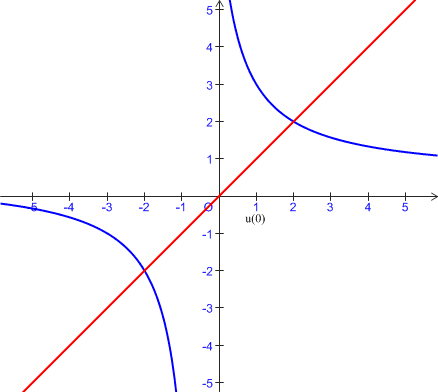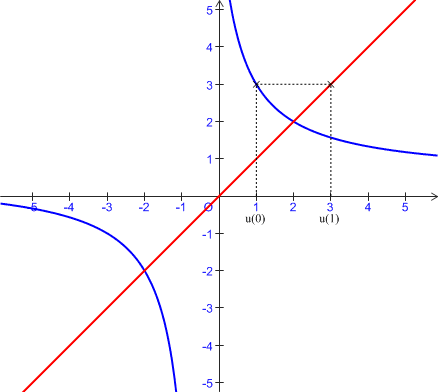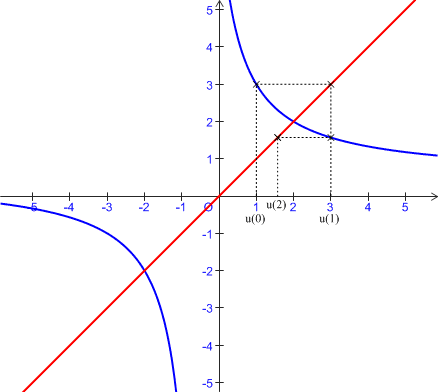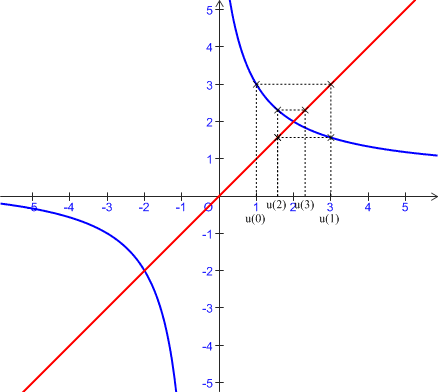
b. Construire à l'aide de
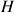et de
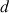les points de l'axe 
d'abscisses respectives
.
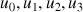Calculer
.
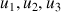c. Que peut-on prévoir quant à la convergence de la suite
?
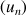2)
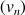est la suite définie pour tout entier naturel
par :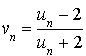 
.
a. Quelle est la nature de la suite
?
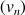b. Exprimer
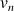en fonction de
.
c. Déterminer la limite de la suite
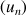quand
tend vers
.
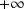