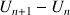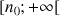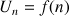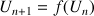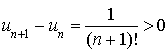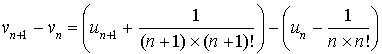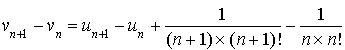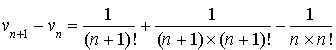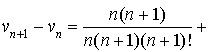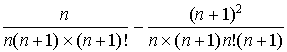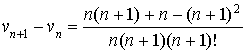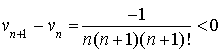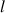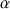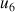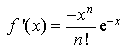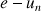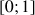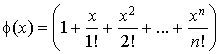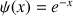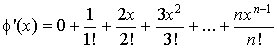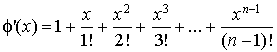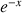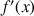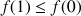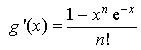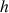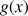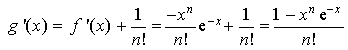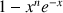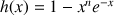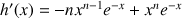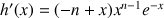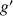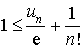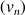Etude de convergence d'une suite définie par une somme
Introduction
Durée : 60 minutes
Niveau : moyen
Première partie
On considère la suite
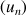définie pour tout entier naturel non nul
par : 
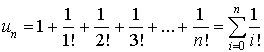
Première partie : la suite
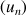est convergente.
On considère la suite
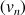définie pour tout entier naturel non nul
par 
.
1) Déterminer le sens de variation des suites
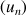et
.
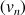2) Calculer la limite de
.
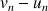4) Donner une valeur approchée par défaut de l à 0,002 près.
Deuxième partie
On considère la suite
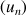définie pour tout entier naturel non nul
par :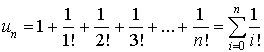
Deuxième partie : la suite
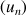converge vers
.
Soit
un entier fixé non nul. On pose pour tout
réel :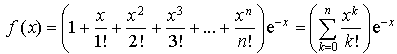 
.
1) Calculer
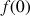et
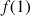. Montrer que la fonction
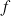est dérivable sur R.
En déduire que
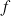est décroissante sur
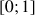, puis que 
.
2) On considère la fonction
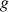définie sur R par 
.
Montrer que
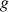est croissante
, et en déduire que 
.
