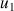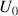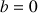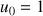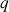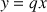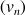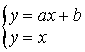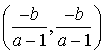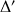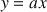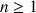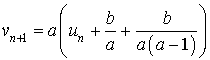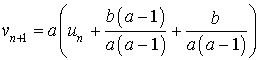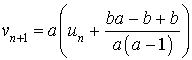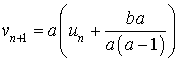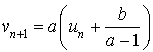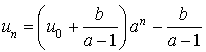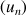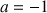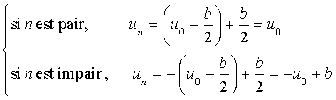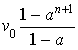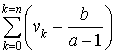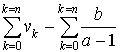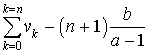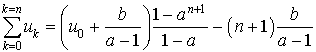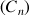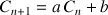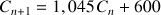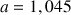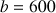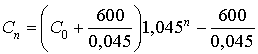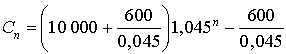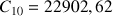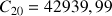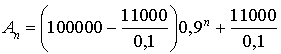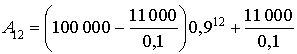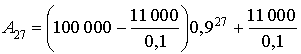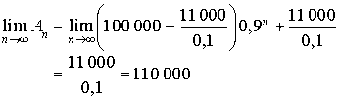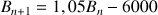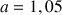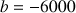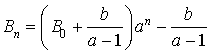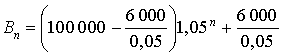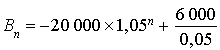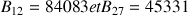Suite avec paramètres
Introduction
Durée : 60 minutes
Niveau : moyen
Suite avec paramètres
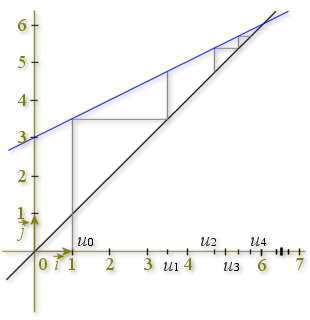
On veut étudier les suites définies par la donnée de
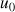et une relation du type 
.
1) Des conjectures...
a. Quelle est la nature de la suite lorsque
?
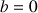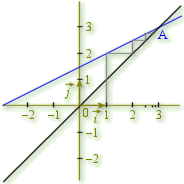
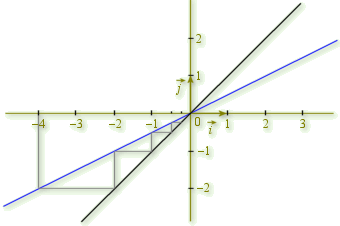
b. Représenter dans un repère orthonormal
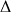la droite d'équation
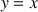, ainsi que la droite
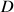d'équation
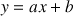(on fera la figure pour 
et
).
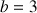Utiliser ce graphique pour déterminer graphiquement les premiers termes de la suite
.
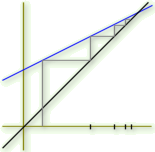
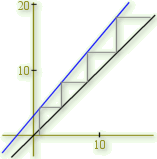
c. Utiliser l'outil graphique mis à votre disposition pour faire la figure pour diverses valeurs de
et
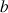. Établir des conjectures sur la convergence de la suite, selon les valeurs de
.
2) Démonstration en utilisant une suite auxiliaire. Expression du terme général.
a. On appelle A le point d'intersection des droites
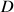et
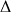. Calculer les coordonnées de
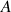. En utilisant la représentation précédente (et l'outil graphique), déterminer un réel
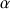(en fonction de
et
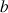) tel que la suite
définie par
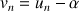soit une suite géométrique ?
b. Exprimer alors
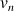, puis
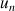, en fonction de
et
.
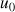c. Etudier la convergence de la suite
.
3) Calculer la somme des termes de la suite
, puis de la suite
.
4) Applications.
a. Placement d'un capital
(type « plan d'épargne » : on place 10 000 € le 1er janvier 2000, à 4,5 %, puis on ajoute tous les ans 600 €).
On note
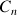le capital acquis au bout de
années.
Exprimer
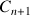en fonction de
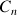, puis
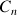en fonction de
.
Calculer
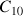et
.
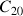b. Dans une ville A de 100 000 habitants au 1er janvier 2003, la population vieillissante se renouvelle peu ; le taux de renouvellement de la population est de 0,9 (c'est-à-dire : le nombre d'habitants, hors migration, est multiplié par 0,9 d'une année sur l'autre). La douceur du climat incite cependant chaque année 11 000 retraités à s'installer dans la belle ville de A.
Au contraire, dans une ville B de 100 000 habitants au 1er janvier 2003, la population est jeune et se renouvelle avec un taux 1,05 (c'est-à-dire le nombre d'habitants est multiplié par 1,05 d'une année sur l'autre). La situation économique difficile contraint cependant chaque année 6 000 personnes à quitter la ville B.
On note
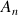le nombre d'habitants de
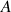au 1er janvier (2003 +
), et
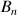le nombre d'habitants de
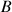à la même date.
Exprimer
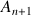en fonction de
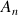, puis en fonction de
.
Calculer la population de la ville
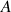au 1er janvier 2015, puis au 1er janvier 2030. Calculer 
. Comment interpréter ce résultat.
Mêmes questions pour la suite
.
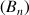