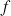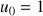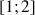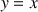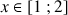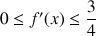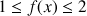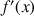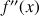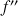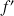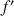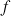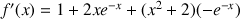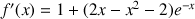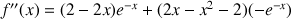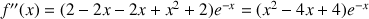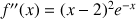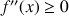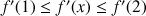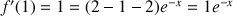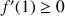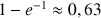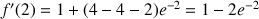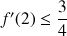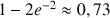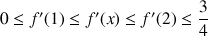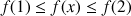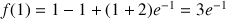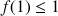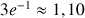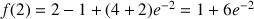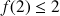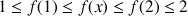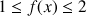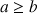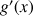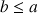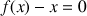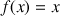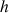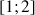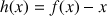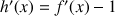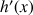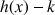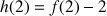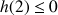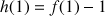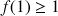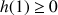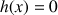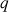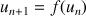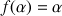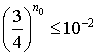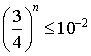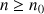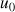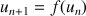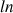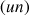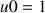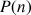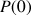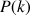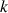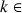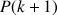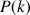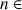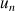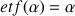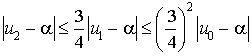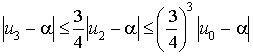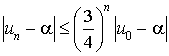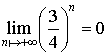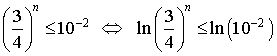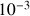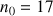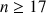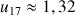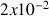Approche d'un point fixe par une suite
Introduction
Durée : 60 minutes
Niveau : difficile
Soit
Soit
La courbe
| 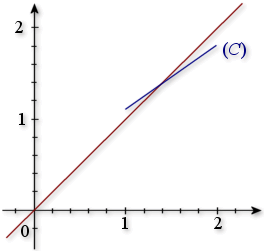 |
2) On considère la fonction
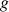 définie par :
définie par : ![]() .
.
Soient
 et
et
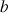 deux réels dans
deux réels dans
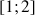 . Démontrer que si
. Démontrer que si
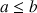 ,
, ![]() .
.
En déduire que pour tout
 et tout
et tout
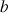 dans
dans
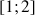 :
: ![]() .
.
3) Démontrer que
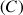 et
et
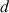 ont un point d'intersection unique.
ont un point d'intersection unique.
On note
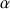 l'abscisse de ce point.
l'abscisse de ce point.
4) a. Démontrer que pour tout entier naturel
 :
: ![]() .
.
b. Démontrer que pour tout entier naturel
 :
: ![]() .
.
En déduire que pour tout entier naturel
 :
: 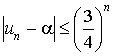 .
.
c. Démontrer que la suite
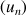 est convergente et donner sa limite.
est convergente et donner sa limite.
d. Trouver un entier
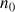 tel que pour tout entier naturel
tel que pour tout entier naturel
 supérieur ou égal à
supérieur ou égal à
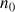 on ait
on ait ![]() .
.
e. Donner une valeur approchée de
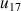 à
à
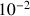 près. En déduire une valeur approchée de
près. En déduire une valeur approchée de
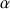 .
.