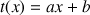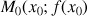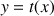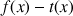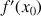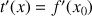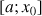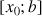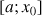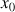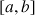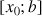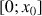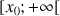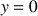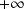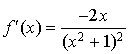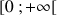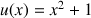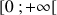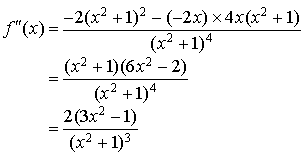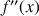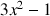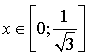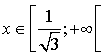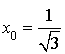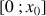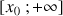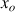Position relative d'une courbe et de sa tangente en un point
Introduction
Durée : 50 minutes
Niveau : moyen
Position relative d'une courbe et de sa tangente en un point
L'objectif de cet exercice est l'étude de la position de la courbe représentative
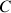d'une fonction
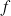et de la tangente à
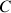au point .
1) Soit
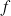une fonction deux fois dérivable sur l'intervalle
(
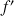et existent
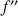) telle que pour tout 
, 
.
On note
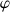la fonction définie sur
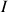par 
où
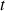est la fonction dont la représentation graphique (
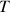) est la tangente à la représentation graphique
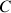de
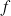en un point (
).
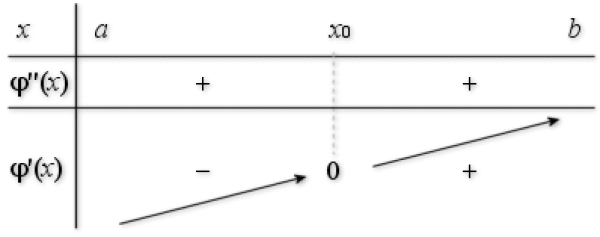
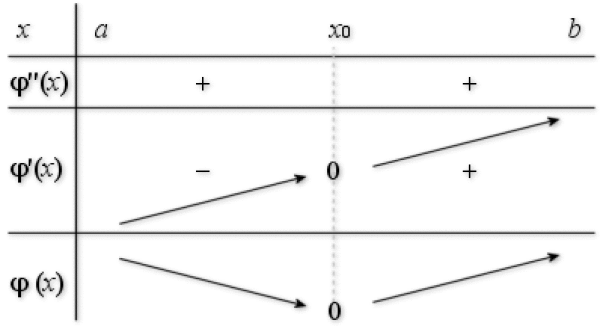
a. Calculer 
et à l'aide des variations de
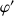déterminer le signe de 
.
b. Montrer que la courbe
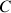représentative de
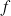est au-dessus d'une quelconque de ses tangentes.
2) Soit
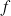une fonction deux fois dérivable sur un intervalle
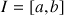et telle que pour tout
, .
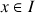Montrer que la courbe représentative de
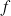est en dessous de l'une quelconque de ses tangentes.
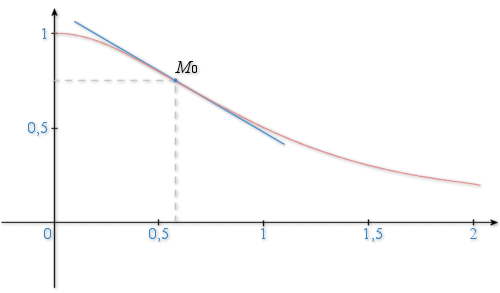
3) On considère la fonction
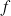définie sur
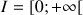par 
.
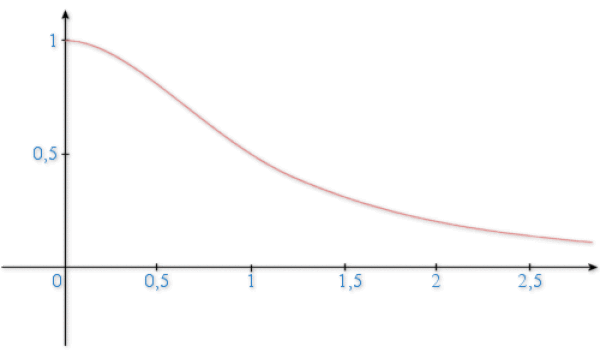
a. Déterminer 
, étudier les variations de
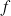puis tracer la représentation graphique de
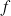dans un repère orthonormal 
(unité de longueur 5cm).
b. Déterminer la fonction
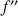dérivée seconde de
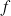puis étudier son signe sur
.
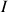c. On désigne par
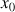le réel unique de
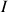tel que
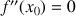et
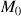le point de coordonnées 
.
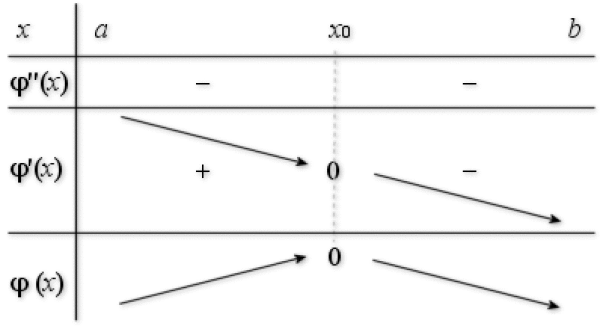
Préciser la position de la représentation graphique de
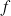par rapport à ses tangentes sur chacun des intervalles
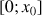et
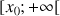; quelle est la position de la représentation graphique de
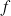par rapport à sa tangente (
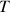) en
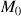. Placer (
).
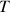